AI/Machine Learning
[ML] Softmax Regression(소프트맥스 회귀)이란?
운호(Noah)
2020. 10. 8. 20:29
이진 분류란?
- 이진 분류란, 문제에 대한 정답을 두 가지 답 중 하나로 분류하는 것을 의미한다.
- 예를 들어, 문제에 대한 정답이 0 과 1 중 하나라면,
- 해당 문제에 대한 정답이 1 일 확률이 출력되고,
- 해당 확률이 0.5 이상이면 1 로 판단한다.
- 이러한 이진 분류 문제를 해결하기 위한 회귀 분석 중 하나가, Logistic Regression 이다.
- Logistic Regression 은, 가설 함수로 시그모이드 함수를 사용하며
- 비용 함수로는 Binary Cross Entropy 를 사용한다.
다중 분류란?
- 다중 분류란, 문제에 대한 정답을 세 가지 이상의 답 중 하나로 분류하는 문제이다.
- 다중 분류 문제에도, 이진 분류에서 사용된 시그모이드 함수를 적용해 정답을 도출할 수 있다.
- 예를 들어, 어떤 문제에 대한 정답이 0, 1, 2 중 하나이고,
- 각 정답에 대해 시그모이드 함수를 적용한다면,
- 해당 문제의 정답이
- 0 일 확률이 0.7,
- 1 일 확률이 0.6,
- 2 일 확률이 0.4 와 같이 나올 수 있다.
- 하지만, 이렇게 되면 전체 정답지의 확률 합이 1 이 넘는다는 문제가 발생하게 된다.
- 따라서, 정답지의 확률 합을 1 이 되도록 만드는 함수가 소프트맥스 함수이며, 이러한 분석을 소프트맥스 회귀라고 한다.
소프트맥스 회귀(Softmax Regression)
소프트맥스 회귀는 가설 함수로 소프트맥스 함수를 사용하며, 비용 함수로는 Cross Entropy 를 사용한다.
소프트맥스 함수 (가설 함수)

- 분류해야하는 클래스의 총 개수가 k 개일 때, k 차원의 벡터 z = [z1, z2, z3]을 입력 받으면
- 소프트맥스 함수는, 위와 같이 각 클래스에 대한 확률 [p1, p2, p3]을 리턴한다.
- p1, p2, p3 는 각각 1번 클래스가 정답일 확률, 2번 클래스가 정답일 확률, 3번 클래스가 정답일 확률이며, 각 확률은 0~1 사이의 값이고 확률들의 총합은 1 이다.
Cross Entropy (비용 함수)
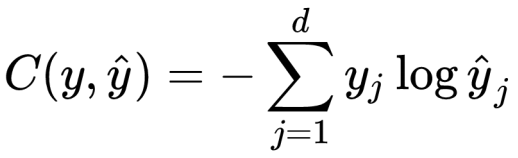
- 예를 들어, 예측 벡터값이 [0.5, 0.2, 0.3] 이고, 실제 벡터값이 [1, 0, 0] 라면
- 해당 공식에 의해 cost 는 -log(0.5) 가 된다.
- Cross Entropy 공식은, 예측 벡터와 실제 벡터 중 정답 값의 오차만 계산하는 의미와 동일하다.
- 예측 벡터의 확률 합은 1 이기 때문에,
- 0.5 라는 확률값을 1 로 맞추기만 한다면, 나머지 확률값들은 0 으로 수렴하기 때문이다.