[ML] 분류 성능 평가 지표 - Precision(정밀도), Recall(재현율), Accuracy(정확도)
- 기계학습에서 모델이나 패턴의 분류 성능 평가에 사용되는 지표들을 다루겠습니다.
- 어느 모델이든, 발전을 위한 feedback은 현재 모델의 performance를 올바르게 평가하는 것에서부터 시작합니다.
- 모델이 평가해야하는 요소와 그것을 수치화한 지표들, 그리고 관련 개념들에 대해서 다루도록 하겠습니다.
모델의 분류와 정답
모델을 평가하는 요소는 결국, 모델이 내놓은 답과 실제 정답의 관계로써 정의를 내릴 수 있습니다.
정답이 True와 False로 나누어져있고, 분류 모델 또한 True False의 답을 내놓습니다.
그렇게 하면, 아래와 같이 2x2 matrix로 case를 나누어볼 수 있겠네요.
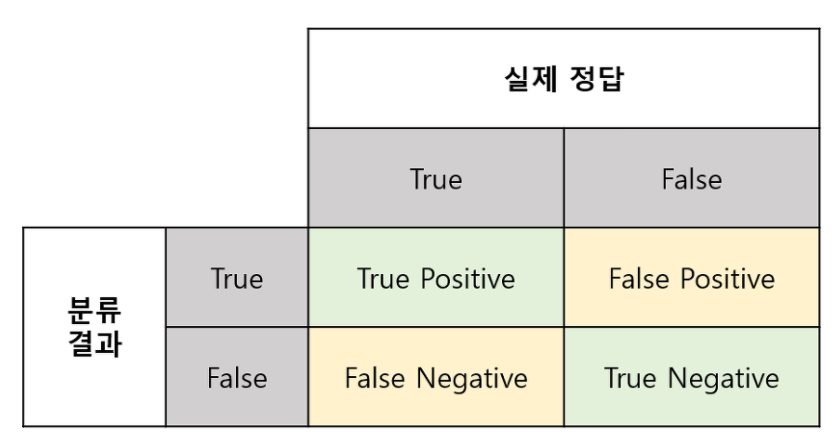
이제 각 case별로 살펴보겠습니다.
- True Positive(TP) : 실제 True인 정답을 True라고 예측 (정답)
- False Positive(FP) : 실제 False인 정답을 True라고 예측 (오답)
- False Negative(FN) : 실제 True인 정답을 False라고 예측 (오답)
- True Negative(TN) : 실제 False인 정답을 False라고 예측 (정답)
이러한 case별로 우리의 분류 모델의 성능을 어떻게 평가할 수 있을까요?
1. Precision(정밀도), Recall(재현율), Accuracy(정확도)
- Precision, Recall, Accuracy는 논문에서도 사용하는 지표들이며 가장 눈에 익는 지표들입니다.
- 하지만 서로 헷갈리는 경우가 많으니, 제대로 정리할 필요가 있겠습니다.
- 우리는 모델이 예측한 다양한 경우를 생각해보며, 위의 2x2 matrix에 해당하는 것을 어떻게 지표화 할 것인지 고민해보겠습니다.
- 지표를 고민함과 동시에 실제 사례를 들어서 해당 지표를 왜 써야하는지도 함께 생각해보고자 합니다.
- 여기서는 한달 동안의 날씨를 예측하는 상황을 생각해보겠습니다.
- 날씨는 비가 오거나 맑거나 두 가지만 존재한다고 가정합니다.
1.1 Precision(정밀도)
정밀도란 모델이 True라고 분류한 것 중에서, 실제 True인 것의 비율입니다.
즉, 아래와 같은 식으로 표현할 수 있습니다.
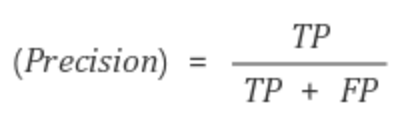
Positive 정답률, PPV(Positive Predictive Value)라고도 불립니다.
날씨 예측 모델이 맑다로 예측했는데, 실제 날씨가 맑았는지를 살펴보는 지표라고 할 수 있겠습니다.
1.2 Recall(재현율)
재현율이란 실제 True인 것 중에서, 모델이 True라고 예측한 것의 비율입니다.
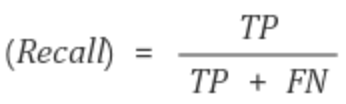
통계학에서는 sensitivity으로, 그리고 다른 분야에서는 hit rate라는 용어로도 사용합니다.
실제 날씨가 맑은 날 중에서 모델이 맑다고 예측한 비율을 나타낸 지표인데, 정밀도(Precision)와 True Positive의 경우를 다르게 바라보는 것입니다.
즉, Precision이나 Recall은 모두 실제 True인 정답을 모델이 True라고 예측한 경우에 관심이 있으나, 바라보고자 하는 관점만 다릅니다.
Precision은 모델의 입장에서, 그리고 Recall은 실제 정답(data)의 입장에서 정답을 정답이라고 맞춘 경우를 바라보고 있습니다.
예를 들어 보겠습니다.
"어떤 요소에 의해, 확실히 맑은 날을 예측할 수 있다면, 해당하는 날에만 맑은 날이라고 예측하면 되겠다."
이 경우에는, 확실하지 않은 날에는 아에 예측을 하지 않고 보류하여 FP의 경우의 수를 줄여, Precision을 극도로 끌어올리는 일종의 편법입니다.
즉, 30일 동안 맑은 날이 20일이었는데, 확실한 2일만 맑다고 예측한다면, 당연히 맑다고 한 날 중에 실제 맑은 날(Precision)은 100%가 나오게 됩니다.
하지만 과연, 이러한 모델이 이상적인 모델일까요?
따라서, 우리는 Recall(재현율)을 통해, 실제 맑은 20일 중에서 예측한 맑은 날의 수도 고려해 보아야합니다.
이 경우에는 Precision만큼 높은 결과가 나오지 않습니다.
따라서, Precision과 함께 Recall을 함께 고려하면 실제 맑은 날들(즉, 분류의 대상이 되는 정의역, 실제 data)의 입장에서 우리의 모델이 맑다고 예측한 비율을 함께 고려하게 되어 제대로 평가할 수 있습니다.
Precision과 Recall은 상호보완적으로 사용할 수 있으며, 두 지표가 모두 높을 수록 좋은 모델입니다.
하지만, Precision과 Recall은 trade-off 관계에 있습니다.
1.3 Precision-Recall Trade-off
Precision과 Recall은 trade-off 관계에 있습니다.
벤다이어그램으로 두 관계를 생각해볼 수 있습니다.
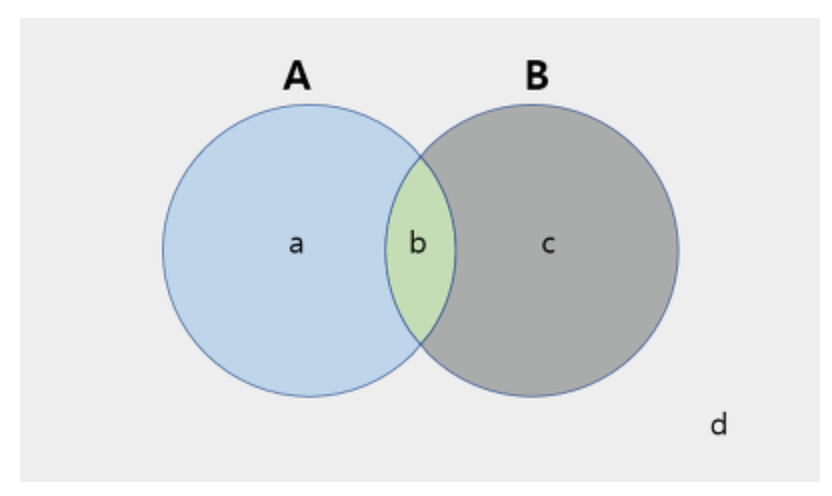
A는 실제 날씨가 맑은 날입니다.
B는 모델에서 날씨가 맑은 날이라고 예측한 것입니다.
이때, b의 영역은 TP로써, 실제 맑은 날씨를 모델이 맑다고 제대로 예측한 영역입니다.
이러한 영역 상에서 Precision과 Recall은 다음과 같습니다.
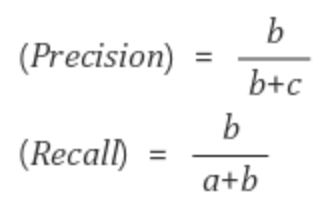
모델의 입장에서 모두 맑은 날이라고만 예측하는 경우를 생각해봅시다.
그렇게 되면 TN(d)의 영역이 줄어들게 되고 그에 따라 FN(a)의 영역 또한 줄게 됩니다.
그러므로 Recall은 분모의 일부인 FN(a)영역이 줄기 때문에 Recall은 100%가 됩니다.
즉, 여기서 A⊂B인 관계를 형성합니다.
하지만, 주의할 것은 단순히 a의 영역만 줄어드는 것이 아니라
d의 영역과 a의 영역이 모두 c로 흡수된다는 것입니다.
Precision의 경우에는 기존보다 FP(c)의 영역이 커져 Precision은 줄게 됩니다.
이해가 안된다면 다음 표로 이해해보겠습니다.

왼쪽의 General Case에서 Recall은 20 / 50 = 40%, Precision = 20 / 60 = 33.3% 입니다.
그리고 분류모델이 모두 True라고 예측한 오른쪽의 case에서의 recall은 FN = 0이므로 100%이지만, 그에 따라 FP가 늘어서 precision은 20/100 = 20%가 되었습니다.
이처럼 precision과 recall은 모두 높은 것이 좋지만, trade-off 관계에 있어서 함께 늘리기가 힘듭니다.
1.4 Accuracy(정확도)
이제는 또 관점을 다르게 생각해봅시다.
사고의 확장이 빠른 사람들은 예상했겠지만, 위 두 지표는 모두 True를 True라고 옳게 예측한 경우에 대해서만 다루었습니다.
하지만, False를 False라고 예측한 경우도 옳은 경우입니다.
이때, 해당 경우를 고려하는 지표가 바로 정확도(Accuracy)입니다. 식으로는 다음과 같이 나타냅니다.

정확도는 가장 직관적으로 모델의 성능을 나타낼 수 있는 평가 지표입니다.
하지만, 여기서 고려해야하는 것이 있습니다.
바로 domain의 편중(bias)입니다.
만약, 우리가 예측하고자 하는 한달 동안이 특정 기후에 부합하여 비오는 날이 흔치 않다고 생각해보죠.
이 경우에는 해당 data의 domain이 불균형하게되므로, 맑은 것을 예측하는 성능은 높지만, 비가 오는 것을 예측하는 성능은 매우 낮을 수 밖에 없습니다.
따라서 이를 보완할 지표가 필요합니다.
1.5 F1 score
F1 score는 Precision과 Recall의 조화평균입니다.

F1 score는 데이터 label이 불균형 구조일 때, 모델의 성능을 정확하게 평가할 수 있으며, 성능을 하나의 숫자로 표현할 수 있습니다.
여기서 단순 산술평균으로 사용하지 않는 이유는 무엇일까요?
우리가 평균 속력을 구할 때, 이 조화평균의 개념을 사용해 본 경험이 있을 것입니다.
조화평균의 본질에 대해 이해해보겠습니다.
조화평균은 기하학적으로 다음과 같이 표현할 수 있습니다.
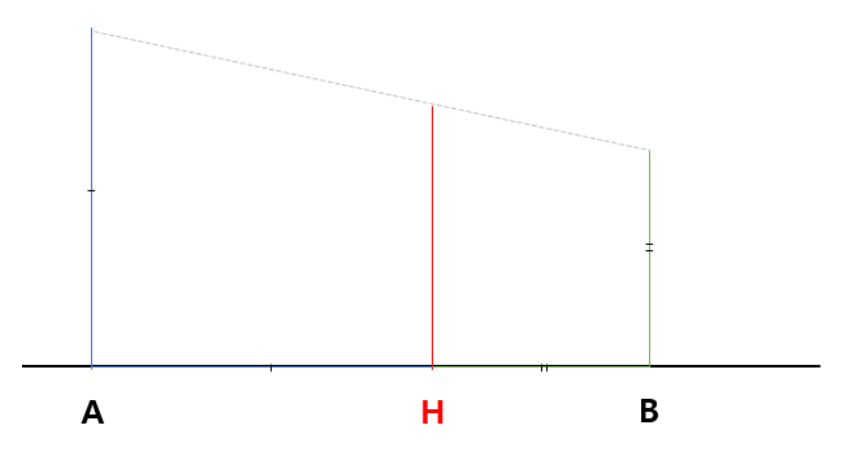
서로 다른 길이의 A, B와 이 두 길이의 합만큼 떨어진 변(AB)으로 이루어진 사다리꼴을 생각해봅시다.
변(AB)에서 각 변의 길이가 만나는 지점(H)으로부터, 맞은 편의 사다리꼴의 변으로 내린 선분이 바로 조화평균을 나타냅니다.
기하학적으로 봤을 때, 단순 평균이라기보다는 길이가 작은 쪽으로 치우치게 된, 그러면서 작은 쪽과 큰 쪽 사이의 값을 가진 평균이 도출됩니다.
이렇게 조화평균을 이용하면 산술평균을 이용하는 것보다, 큰 비중이 끼치는 bias가 줄어든다고 볼 수 있습니다
즉, F1-score는 아래와 같이 생각할 수 있습니다.
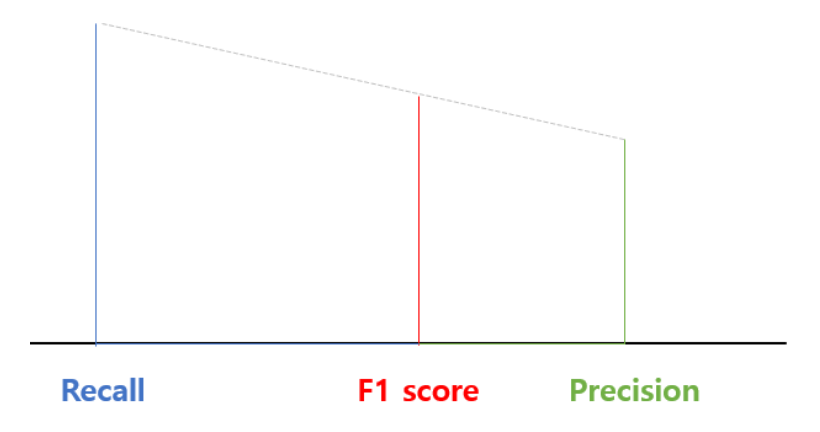
2. 그 외 다른 지표들
- 이 외에도 모델의 성능을 측정하는 다양한 지표들이 존재합니다. 다음을 살펴봅시다.
2.1 Fall-out
- Fall-out은 FPR(False Positive Rate)으로도 불리며,
- 실제 False인 data 중에서, 모델이 True라고 예측한 비율입니다.
- 즉, 모델이 실제 false data를 True라고 잘못 예측한 것으로, 다음과 같이 표현할 수 있습니다.
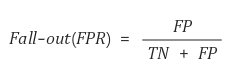
2.2 ROC(Receiver Operating Characteristic) curve
- ROC curver는 여러 임계값들을 기준으로 Recall-Fallout의 변화를 시각화한 것입니다.
- Recall은 실제 True인 data 중에서 모델이 True로 분류한 비율을 나타내며,
- Fall-out은 실제 False인 data 중에서 모델이 True로 분류한 비율을 나타냅니다.
- 이 두 비율을 각각 x, y 축으로 놓고 그려지는 그래프를 해석합니다.
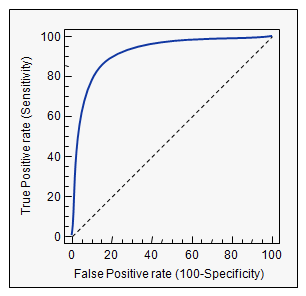
- curve가 왼쪽 위 모서리에 가까울수록 모델의 성능이 좋다고 평가합니다.
- 즉, Recall이 크고 Fall-out이 작은 모형이 좋은 모형인 것입니다.
- 또한 y=x 그래프보다 상단에 위치해야 어느정도 성능이 있다고 말할 수 있습니다.
2.3 AUC(Area Under Curve)
- ROC curve는 그래프이기 때문에 명확한 수치로써 비교하기가 어렵습니다.
- 따라서 ROC curve 그래프 아래의 면적값을 이용합니다.
- 이것이 바로 AUC(Area Under Curve)입니다.
- 최대값은 1이며, 좋은 모델(즉, Fall-out에 비해 Recall 값이 클수록) 1에 가까운 값이 나옵니다.