[ML] Binary Cross Entropy 와 Cross Entropy 의 차이
들어가기 앞서,
- Binary Cross Entropy 와 Cross Entropy 의 개념은 자주 헷갈리는 것 같습니다.
- 따라서, 해당 포스트에서는 Binary Cross Entropy 와 Cross Entropy 의 차이점에 대해서 다뤄볼 것입니다.
진행 순서
- 이진 분류
- 멀티 이진 분류
- 다중 분류
이진 분류
이진 분류란, 데이터가 주어졌을 때, 해당 데이터를 두 가지 정답 중 하나로 분류하는 것을 의미합니다.
- 예를 들어, 홍길동이라는 데이터가 주어졌을 때,
- 해당 데이터가 사람이냐 아니냐에 대한 정답이 1 과 0 중 하나라면,
- 해당 데이터가 1 일 확률이 출력되고,
- 해당 확률이 0.5 이상이면, 1 로 판단하게 됩니다.
Binary Cross Entropy Loss (이진 교차 엔트로피 손실)
이러한 이진 분류에는, Binary Cross Entropy Loss 함수를 활용할 수 있습니다.
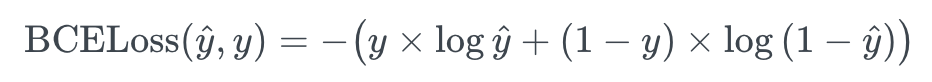
위 Binary Cross Entropy Loss 수식에서 y hat 은, 0 과 1 사이의 연속적인 시그모이드 함수 출력값을 의미하며, y 는 불연속적인 실제값을 의미합니다.
따라서, 단일 항목에 대한 Binary Cross Entropy Loss 는 아래 공식으로 계산할 수 있습니다.
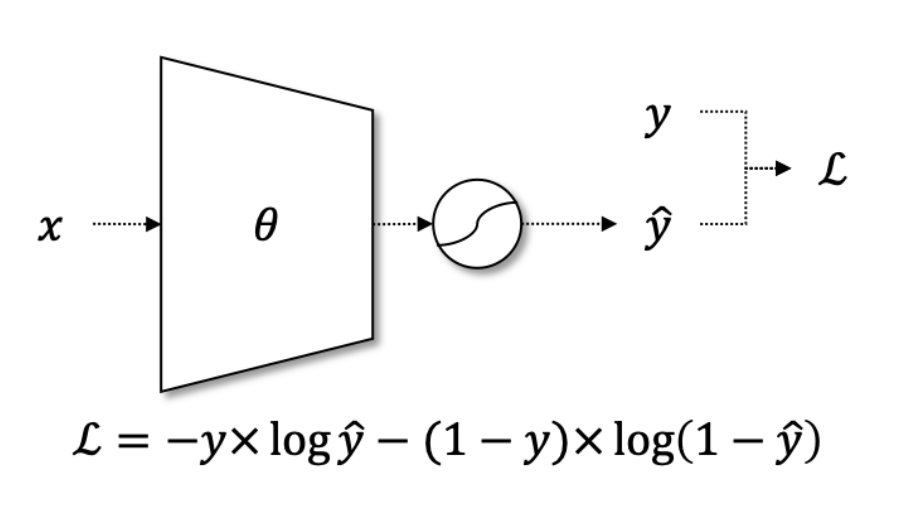
멀티 이진 분류
위 이진 분류에서는, 데이터가 주어졌을 때, 해당 데이터가 사람이냐 아니냐에 대한, 단일 항목에 대해서만 이진 분류를 진행했었습니다.
하지만, 만약 질문 항목이 여러개이며, 각 항목의 대한 정답이 두 가지라면, 이를 멀티 이진 분류라고 합니다.
- 예를 들어, 홍길동이라는 데이터가 주어졌을 때
- 첫 번째 질문 항목은 사람이냐 아니냐,
- 두 번째 질문 항목은 서울에 사느냐, 살지 않느냐로 해당 데이터를 분류할 수 있습니다.
신경망 마지막 계층의 n 개 노드에 대해, 모두 시그모이드 함수를 적용하면, 아래 그림과 같은 모델 구조를 가지며, n 개 항목에 대한 이진 분류 작업을 수행할 수 있습니다.
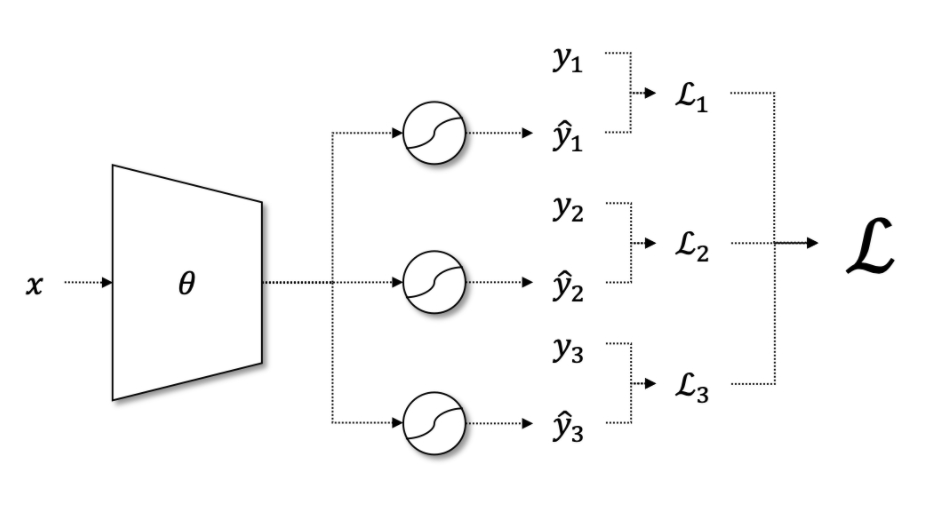
따라서, 다중 항목에 대한 Binary Cross Entropy Loss 는 아래 공식으로 계산할 수 있습니다.

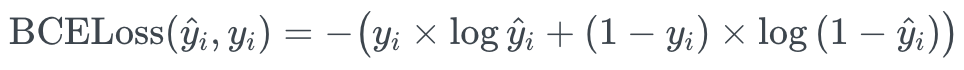
다중 분류
만약, 데이터가 주어졌을 때, 질문 항목은 1개이지만, 해당 항목에 대한 정답은 세 가지 이상이라면, 이를 다중 분류라고 합니다.
- 예를 들어, 홍길동이라는 데이터가 주어졌을 때
- 해당 데이터를 키가 크냐, 중간이냐, 작냐 로 분류할 수 있습니다.
이때는 어쩔 수 없이 sigmoid 함수가 아닌 softmax 함수가 필요하게 됩니다.
만약, 질문 항목이 n 개 이며, 각 항목에 대한 정답이 세 가지 이상이라면,
각 질문에 대해 각각 softmax 함수를 적용해, 아래 그림과 같은 모델 구조를 가지게 되며,
여러 항목에 대한 다중 분류 작업을 수행할 수 있습니다.
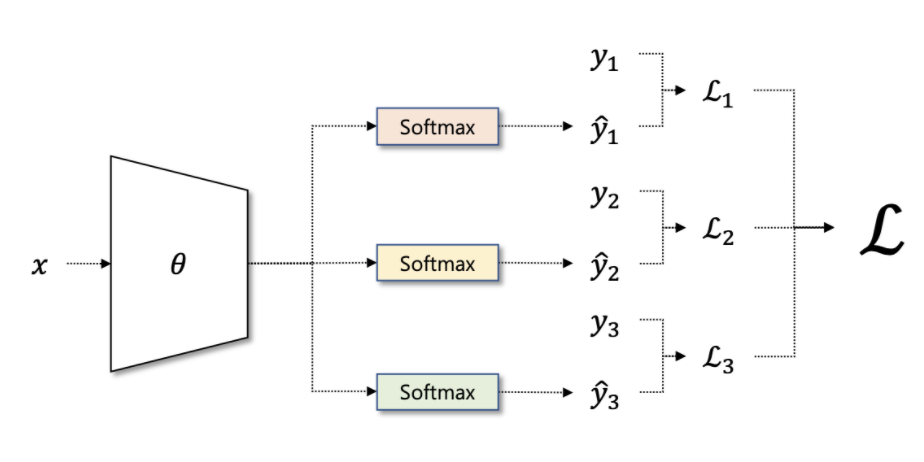
Cross Entropy (교차 엔트로피)
따라서, 다중 분류에 대한 Cross Entropy 는 아래 공식으로 계산할 수 있습니다.

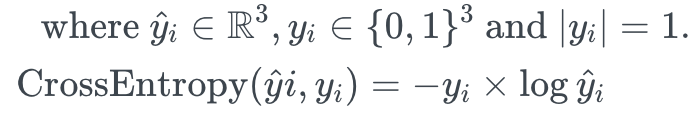
결론
- 예측값이 단일 항목으로 이루어져있다면 (ex, [0.5])
- 단순 이진 분류이므로, 목적함수로 Binary Cross Entropy 를 사용
- 예측값이 여러개의 항목으로 이루어져있으며, 각 항목의 확률 합이 1 이 넘어간다면 (ex, [0.7, 0.6, 0.4])
- 멀티 이진 분류이므로, 목적함수로 Binary Cross Entropy 를 사용
- 예측값이 여러개의 항목으로 이루어져있으며, 각 항목의 확률 합이 1 이라면 (ex, [0.5, 0.2, 0.3])
- 다중 분류이므로, 목적함수로 Cross Entropy 를 사용