우노
[ML] 주성분 분석(PCA, Principal Component Analysis)이란? 본문
주성분 분석(PCA, Principal Component Analysis)
- 데이터의 차원이 커지면 커질수록 계산 복잡도와 정확도가 떨어진다.
- 다차원 데이터를 설명할 수 있는 핵심 축을 찾는다면, 작은 차원으로 모든 데이터를 설명할 수 있다.
- 데이터를 작은 차원으로 줄이는 방법 중 한 가지가 PCA이다.
차원 축소
차원 축소 방법
데이터가 아래와 같이 구성되어 있을 때, 어떤 차원으로 축소할 수 있을까?

방법 1) 아무 차원이나 지운다.
차원을 지운 후, 나머지 데이터를 사영시켰을 때, 분산을 최대화 하는 축을 사용한다.
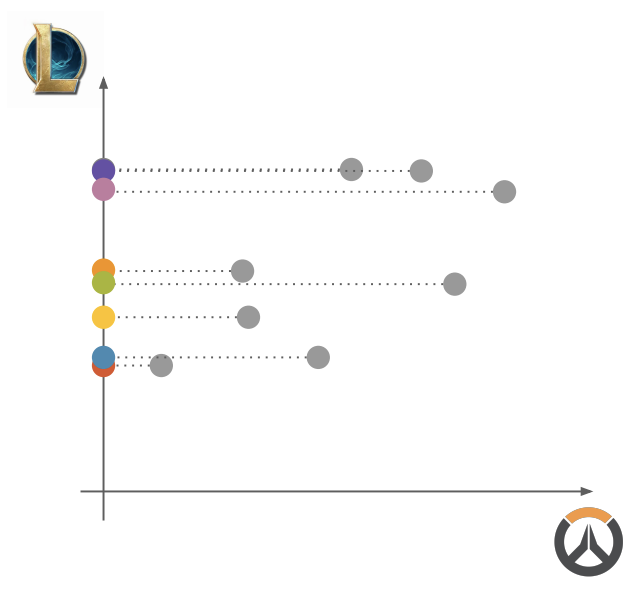

방법 2) 기존의 축이 아닌 새로운 축을 찾는다 ⇒ 주 성분 찾기
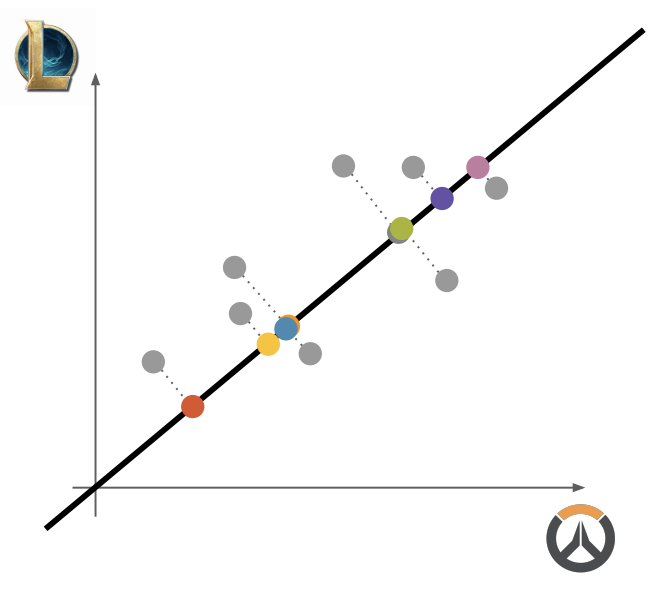
- 기존의 축이 아닌 새로운 축에 사영해, 분산을 최대로 하는 축을 구한다.
- 축은 어떻게 구하는가?
- 아무 축이나 찾고, 분산을 계산해
- 축, 분산 loss function에서 Garadient Descent를 계산한 뒤
- 분산이 커지는 쪽으로 축을 움직인다.
주성분 찾기
분산 구하기
기존 방식

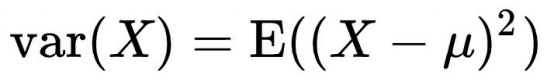
- 점들을 구한 축에 사영한 뒤
- 사영된 점과 점들의 평균 간 거리를 통해 분산을 구했다.
- 하지만, 사영 된 점과 평균 간 거리를 어떻게 구할 수 있을까?
새로운 방식
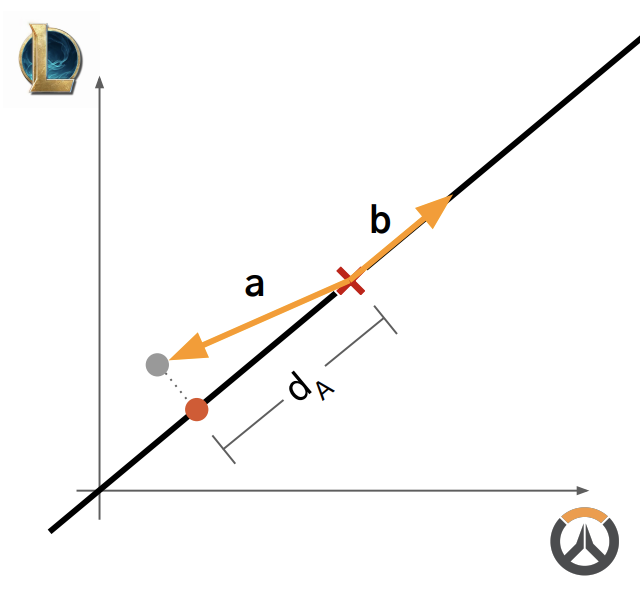
- 주성분 축 방향 벡터를 b 라고 하고, b를 단위벡터라고 한다.
- 평균에서 사영 되기 전의 점까지의 벡터를 a 라고 한다면
- a 벡터와 b 벡터의 내적 = |a|cosΘ * |b| = 거리
- 이렇게 구할려면, 계속 점들의 평균으로부터 벡터를 구한 뒤 내적을 계산해야하므로 귀찮다.
더 쉬운 방식

- 점들의 평균으로부터 벡터를 구한 뒤 내적을 계산하는 작업을 줄이고자
- 점들의 평균을 원점으로 옮겨서 계산한다.
- 이렇게 되면, 벡터 내적을 통해 원점에서 평균 간 거리를 바로 구할 수 있다.
두 번째 주성분 찾기
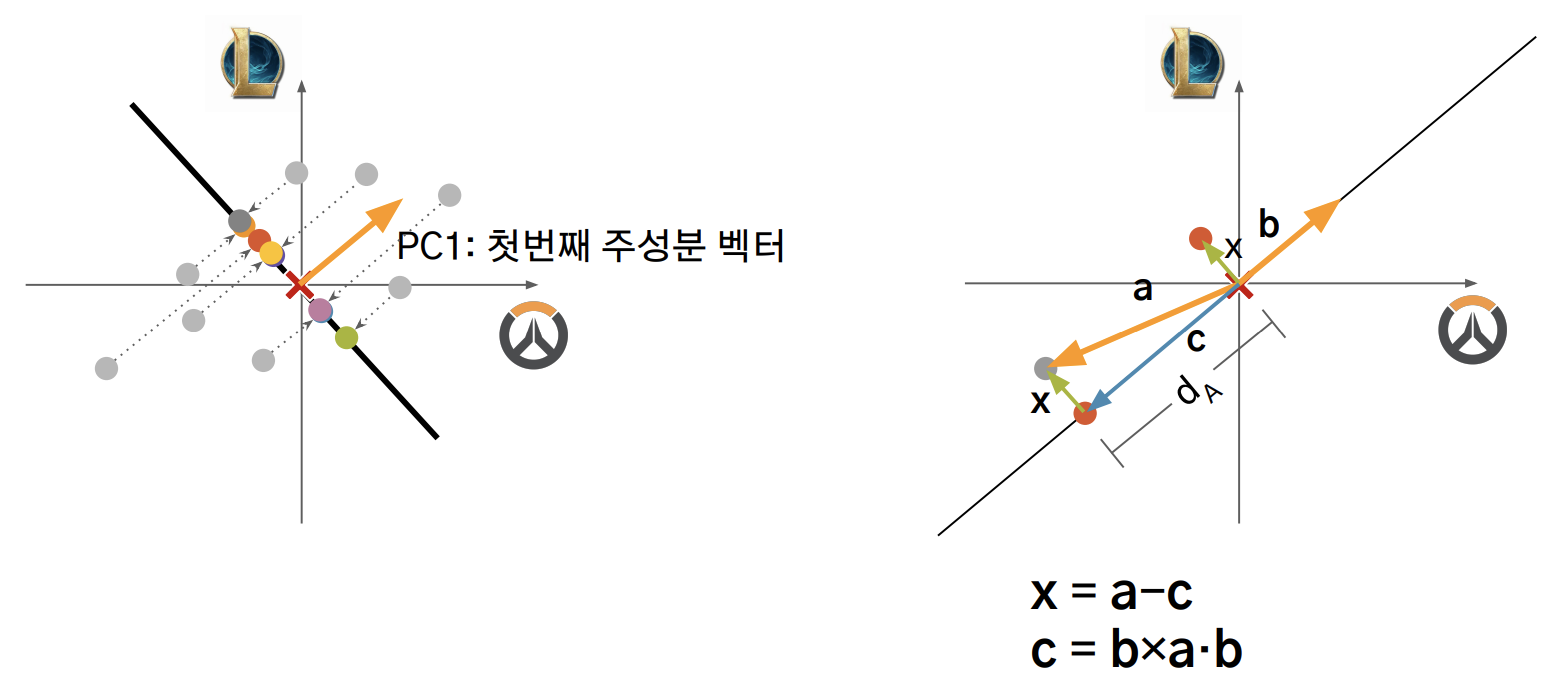
- 첫 번째 주성분 벡터를 찾았다면
- 기존 데이터에서 첫 번째 주성분을 제거한다.
- 첫 번째 주성분을 제거하면 점들은 해당 벡터와 수직인 축에 사영된다.
- 이후, 해당 벡터와 수직인 축에 사영된 점들의 분산을 계산한다.
- 이 때, x를 계산해야한다.
- x = a - c
- c = b x a ⋅ b
3차원 예시

- 순서
- 1) PC1 찾기
- 2) PC1의 직교평면에서 PC2 찾기
- 3) PC1과 PC2에 모두 직교하는 벡터 = PC3
- 각 주성분 축에서 분산값을 기록한 뒤, 일정한 분산 값 이상을 가지는 축만 선택한다.
'AI > Machine Learning' 카테고리의 다른 글
| [ML] Sklearn cross_val_score Custom Scoring 사용하기 (0) | 2021.01.04 |
|---|---|
| [ML] Xgboost Error 해결 방법 (0) | 2021.01.04 |
| [ML] sklearn LinearRegression 튜토리얼 (0) | 2020.11.11 |
| [ML] K-평균(K-Means)이란? (0) | 2020.11.02 |
| [ML] Softmax Regression(소프트맥스 회귀)이란? (0) | 2020.10.08 |
Comments

