우노
[Algorithm] 포드-풀커슨과 에드몬드-카프 알고리즘 본문
최대 유량 문제 (Maximum Flow Problem)
- 특정한 지점에서 다른 지점으로, 얼마나 많은 유량(flow)을 동시에 보낼 수 있는지 계산하는 문제입니다.
- 네트워크 플로우(Network Flow)라고도 합니다.
기본 용어
- 용량 (Capacity)
- c(u, v) : 정점 u 에서 v 로 전송할 수 있는 최대 용량
- 유량 (Flow)
- f(u, v) : 정점 u 에서 v 로 실제 흐르고 있는 유량
- 잔여 용량 (Residual Capacity)
- r(u, v) = c(u, v) – f(u, v)
- 간선의 용량과 살제로 흐르는 유량의 차이
- 소스 (Source)
- s : 모든 유량이 시작되는 정점
- 싱크 (Sink)
- t : 모든 유량이 도착하는 정점
- 증가 경로
- 소스에서 싱크로 유량을 보낼 수 있는 경로
기본 속성
- 용량 제한 속성
- f(u, v) ≤ c(u, v)
- 유량은 용량보다 작거나 같습니다.
- f(u, v) ≤ c(u, v)
- 유량의 대칭성
- f(u, v) = -f(v, u)
- u 에서 v 로 유량이 흐르면, v 에서 u 로 음수의 유량이 흐르는 것과 동일합니다.
- f(u, v) = -f(v, u)
- 유량의 보존성
- 각 정점에 들어오는 유량과 나가는 유량은 같습니다.
기존 최대 유량 탐색 방법의 문제점
예를 들어, 아래 그림과 같은 네트워크가 있다고 가정해봅시다.

- 프로그램은 S 에서 T 로 가는 모든 경로를 탐색하며, 최대 유량을 계산할 것입니다.
- S → a → T
- S → a → b → T
- S → b → T
- 프로그램은 S 에서 T 로 가는 모든 경로를 탐색하며, 최대 유량을 계산할 것입니다.
만약, 프로그램이 아래 그림과 같이, S → a → T 와 S → b → T 의 경로를 먼저 탐색하게 된다면,

- 해당 네트워크의 최대 유량은 2 가 되며, 프로그램은 정답을 맞추게 됩니다.
하지만, 만약 프로그램이 아래 그림과 같이, S → a → b → T 의 경로를 가장 먼저 탐색하게 된다면,
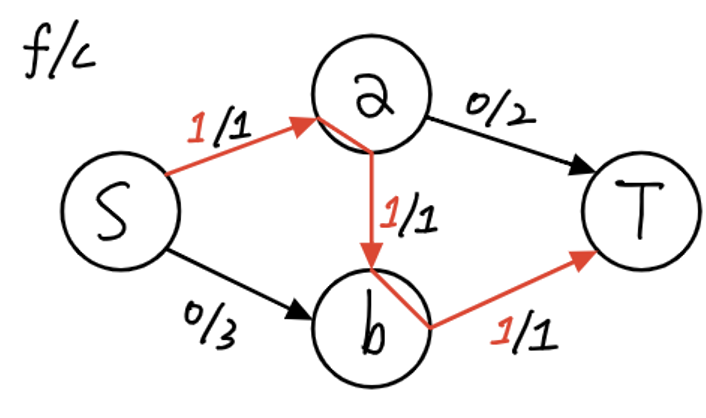
- S → a , a → b, b → T 간선의 유량이 최대치이기 때문에,
- S → b 에 추가로 연결된 경로를 찾지 못하고,
- 최대 유량이 1 인 상태에서 프로그램은 중지되게 됩니다.
그렇다면, 해당 문제는 어떻게 해결할 수 있을까요?
해당 문제는 유량 상쇄를 통해 해결할 수 있습니다.
유량 상쇄
- 유량 상쇄란, 모든 경로에, 기존에 존재하는 간선들과 반대되는 방향의 간선을 추가한 뒤,
- 각 간선으로 유량을 흘려보냈을 때, 반대 방향의 간선으로도 음의 유량을 흘려보냄으로써, 유량을 상쇄시키는 것을 의미합니다.
- 물론, 실제로는 불가능한 얘기이지만, 음의 유량을 기록함으로써, 잔여 용량을 남겨, 추가적인 경로를 탐색할 수 있도록 하기 위한 작업입니다.
- 예를 들어, a → b 의 간선이 존재하며, 유량 f(a, b) 은 1 , 용량 c(a, b) 은 1 이라면,
- 역간선 b → a 의 유량 f(b, a) 은 기존 간선의 방향과 반대이므로 - 1 이 되며,
- 용량 c(b, a) 은 실제 존재하는 간선이 아니므로 0 이 됩니다.
- 따라서, 역간선 b → a 의 잔여 용량 r(b, a) 은, c(b,a) - f(b, a) = 0 - ( - 1 ) = 1 이 됩니다.
- 즉, 역간선 b → a 로 1 의 유량을 추가적으로 흘려보낼 수 있게 됩니다.
- 해당 규칙은, 두 정점이 서로에게 유량을 보내주는 것은 의미가 없기 때문에 성립할 수 있으며,
- 소스에서 싱크로 가는 총 유량도 변하지 않습니다.
최대 유량 알고리즘 종류 및 진행 순서
- 포드-풀커슨 알고리즘 (Ford-Fulkerson Algorithm)
- 네트워크에 존재하는 모든 간선의 유량을 0 으로 초기화하고, 역방향 간선의 유량도 0 으로 초기화합니다.
- 소스에서 싱크로 갈 수 있는, 잔여 용량이 남은 경로를 DFS 로 탐색합니다.
- 해당 경로에 존재하는 간선들의 잔여 용량 중, 가장 작은 값을 유량으로 흘려보냅니다.
- 해당 유량에 음수값을 취해, 역방향 간선에도 흘려보냅니다. (유량 상쇄)
- 더 이상 잔여 용량이 남은 경로가 존재하지 않을때까지 반복합니다.
- 에드몬드-카프 알고리즘 (Edmonds-Karp Algorithm)
- 네트워크에 존재하는 모든 간선의 유량을 0 으로 초기화하고, 역방향 간선의 유량도 0 으로 초기화합니다.
- 소스에서 싱크로 갈 수 있는, 잔여 용량이 남은 경로를 BFS 로 탐색합니다.
- 해당 경로에 존재하는 간선들의 잔여 용량 중, 가장 작은 값을 유량으로 흘려보냅니다.
- 해당 유량에 음수값을 취해, 역방향 간선에도 흘려보냅니다. (유량 상쇄)
- 더 이상 잔여 용량이 남은 경로가 존재하지 않을때까지 반복합니다.
포드-풀커슨 알고리즘 (Ford-Fulkerson Algorithm)
아래 그림을 통해 이해해보겠습니다.

- 위 그림은, 네트워크에 존재하는 모든 간선의 유량을 0 으로 초기화하고, 역방향 간선의 유량도 0 으로 초기화한 뒤
- DFS 를 사용해, 소스에서 싱크로 갈 수 있는 경로 중 하나인 , S → a → b → T 경로를 탐색하고
- 해당 경로에 존재하는 간선들의 잔여 용량 중, 가장 작은 값인 1 을 유량으로 흘려보낸 뒤,
- 해당 유량에 음수값을 취해, 역방향 간선에도 -1 을 흘려보낸 결과입니다.
- 즉, b 에서 a 로, 1 만큼의 유량을 추가로 흘려보낼 수 있는 것을 알 수 있습니다.
따라서, s → b → a → t 경로에 존재하는 간선들의 잔여 용량을 확인한 뒤, 잔여 용량 중 가장 작은 값인 1 을, 유량으로 흘려보냅니다.
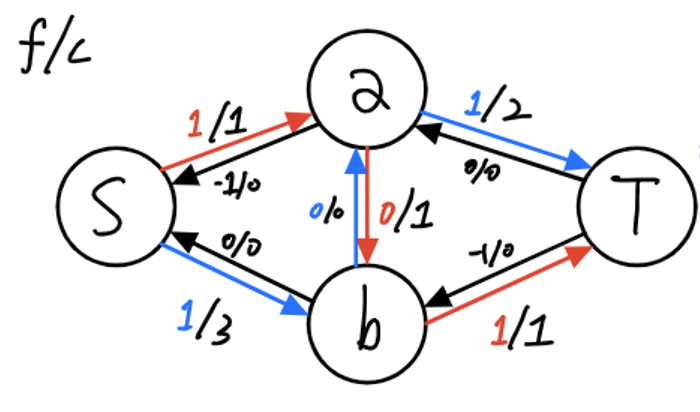
결과적으로, 간선 (a, b) 와 (b, a) 가 상쇄되므로, 아래와 같은 정답이 도출되는 것을 알 수 있습니다.

에드몬드-카프 알고리즘 (Edmonds-Karp Algorithm)
S 부터 T 까지의 증가 경로를 찾을 때, DFS 가 아닌 BFS 를 사용하는 알고리즘입니다.
예제 코드
#include <iostream> #include <vector> #include <queue> #define MAX 100 #define INF 1000000000 using namespace std; int n = 6; // 정점 수 int capacity[MAX][MAX]; // 용량 배열 int flow[MAX][MAX]; // 현재 유량 배열 int visited[MAX]; // 현재 정점 방문 여부 int result; // 최대 유량 결과 // 각 정점이 어느 정점으로부터 방문되었는지 기록하는 배열 vector<int> adj[MAX]; // 최대 유량 계산 void maxFlow(int source, int sink) { while (1) { // 현재 정점 방문 여부 배열을 -1 로 초기화 fill(visited, visited + MAX, -1); // queue 생성 후, source push queue<int> q; q.push(source); // source 에서 sink 로 최단으로 도달하는 경로 찾기 while (!q.empty()) { // queue 의 front 에 위치한 정점 추출 int start = q.front(); q.pop(); // queue 의 front 에 위치한 정점과 인접한 정점 탐색 for (int i = 0; i < adj[start].size(); i++) { // 인접 정점 int end = adj[start][i]; // 인접 정점이, 잔여 용량이 남아있는지 확인하고, 방문하지 않았는지 확인 if (capacity[start][end] - flow[start][end] > 0 && visited[end] == -1) { // 인접 정점으로부터 연결된 경로들을 확인하기 위해, 인접 정점을 queue 에 삽입 q.push(end); // 인접 정점이 어느 정점으로부터 연결되어있는지 기억 visited[end] = start; // 인접 정점이 도착지일 경우, 하나의 증가 경로를 찾았으므로, 더 이상 탐색하지 않고 종료 if (end == sink) break; } } } // sink 까지의 경로를 못 찾았다면, 더 이상의 증가 경로가 없음 if (visited[sink] == -1) break; // 연결된 경로들을 도착지점부터 반대로 모두 확인하며, 최소 유량을 탐색 int f = INF; for (int i = sink; i != source; i = visited[i]) { // min(최소유량, 용량(이전노드, 현재노드) - 유량(이전노드, 현재노드)) f = min(f, capacity[visited[i]][i] - flow[visited[i]][i]); } // 증가 경로는 유량 증가, 역 방향 경로는 유량 감소 for (int i = sink; i != source; i = visited[i]) { // 유량(이전노드, 현재노드) += f flow[visited[i]][i] += f; // 유량(현재노드, 이전노드) -= f flow[i][visited[i]] -= f; } // 최대 유랑 추가 result += f; } } int main() { adj[1].push_back(2); // 간선 추가 adj[2].push_back(1); // 역간선 추가 capacity[1][2] = 14; // 용량 추가 adj[1].push_back(4); adj[4].push_back(1); capacity[1][4] = 12; adj[2].push_back(3); adj[3].push_back(2); capacity[2][3] = 5; adj[2].push_back(4); adj[4].push_back(2); capacity[2][4] = 4; adj[2].push_back(5); adj[5].push_back(2); capacity[2][5] = 6; adj[2].push_back(6); adj[6].push_back(2); capacity[2][6] = 10; adj[3].push_back(6); adj[6].push_back(3); capacity[3][6] = 8; adj[4].push_back(5); adj[5].push_back(4); capacity[4][5] = 11; adj[5].push_back(3); adj[3].push_back(5); capacity[5][3] = 4; adj[5].push_back(6); adj[6].push_back(5); capacity[5][6] = 7; // 1 에서 6 으로 흐르는 최대 유량 탐색 maxFlow(1, 6); // 최대 유량 : 25 printf("최대 유량 : %d\n", result); }
포드-풀커슨 알고리즘 vs 애드몬드-카프 알고리즘
포드-풀커슨 알고리즘은 DFS 방식으로 증가 경로를 찾고,
에드몬드-카프 알고리즘은 BFS 방식으로 증가 경로를 찾습니다.
하지만, DFS 를 통해 경로를 탐색하는 방법은, 비효율적으로 동작할 수 있는 경우가 있습니다.
그림을 통해 이해해보겠습니다.

- 위 그림에서, DFS 를 이용한 증가 경로 탐색은 아래와 같습니다.
- A→B→C→D (1의 유량 보냄)
- A→C→B→D (역간선을 이용해 1의 유량 보냄)
- A→B→C→D (1의 유량 보냄)
- A→C→B→D (역간선을 이용해 1의 유량 보냄)
- 반복
- BFS 를 이용한 증가 경로 탐색 결과는 아래와 같습니다.
- A→B→D (1000의 유량 보냄)
- A→C→D (1000의 유량 보냄)
- 즉, DFS 는 2000 번의 탐색으로 최대 유량을 찾아냈지만,
- BFS 는 2번의 탐색으로 최대 유량을 찾아냈습니다.
- 위 그림에서, DFS 를 이용한 증가 경로 탐색은 아래와 같습니다.
따라서, 애드몬드-카프 알고리즘이 일반적으로 더 효율적으로 동작하는 것을 알 수 있습니다.
물론, 포드-풀커슨의 시간복잡도는 O( (|E|+|V|) * F ) 이고, 애드몬드-카프의 시간복잡도는 O( |V| * (|E|^2) ) 이므로,
- E : 간선
- V : 정점
- F : 최대 유량
문제의 Flow(최대 유량)가 적고, Edge(간선)가 많으면 오히려 포드-풀커슨 알고리즘이 효율적일 수 있습니다.
참고
'Algorithm > Concept' 카테고리의 다른 글
| [Algorithm] DFS 와 BFS 의 동작 과정 간단 비교 (0) | 2022.06.05 |
|---|---|
| [Algorithm] N 의 범위에 따른 시간 복잡도 선택 (0) | 2022.05.27 |
| [Algorithm] 너비 우선 탐색(BFS)이란? (2) | 2022.01.18 |
| [Algorithm] 다익스트라(Dijkstra) 알고리즘 (2) | 2021.12.08 |
| [Algorithm] PageRank 란? (0) | 2020.12.07 |



