오늘의 인기 글
최근 글
최근 댓글
Today
Total
01-02 02:44
관리 메뉴

우노

[Algorithm] 정렬 알고리즘 종류 본문

Algorithm/Concept

[Algorithm] 정렬 알고리즘 종류

운호(Noah) 2022. 6. 6. 22:18

선택 정렬

  • 개념

    • 정렬 되지 않은 데이터들 중 가장 작은 데이터를 선택하고, 정렬 되지 않은 데이터들 중 가장 왼쪽에 있는 데이터와 교환하는 알고리즘입니다.

  • 특징

    • 시간복잡도는 현재 데이터의 정렬 상태와 상관이 없습니다.

  • 시간복잡도

    • 항상 O(N^2)
      • 매번, 정렬 되지 않은 데이터들을 비교 연산하며, 가장 작은 수를 찾습니다.
        • N + (N - 1) + (N - 2) + … + 2 = N x (N-1 ) / 2
      • 가장 작은 수를 찾아서 데이터를 교환합니다.
        • N - 1
      • 두 시간 복잡도를 더하면, O(N^2) 가 됩니다.

  • 구현 코드

      array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

  for i in range(len(array)):
      min_index = i # 가장 작은 원소의 인덱스
      for j in range(i + 1, len(array)):
          if array[min_index] > array[j]:
              min_index = j
      array[i], array[min_index] = array[min_index], array[i] # 스와프

  print(array)

삽입 정렬

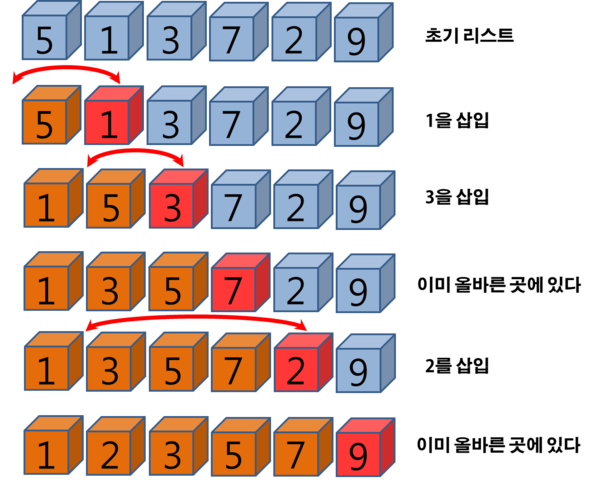
  • 개념

    • 정렬 되지 않은 데이터들 중 가장 왼쪽에 있는 데이터를, 현재까지 정렬한 데이터들 사이에 적절하게 삽입하는 알고리즘입니다.

  • 특징

    • 입렫 받은 리스트의 데이터가 거의 정렬 되어 있을 때, 매우 빠르게 동작합니다.

  • 시간복잡도

    • Best : O(N)
      • 현재까지 정렬한 데이터들 사이에 넣을 필요가 없기 때문입니다.
    • Worst : O(N^2)
      • 모든 데이터가 반대로 정렬되어 있는 경우를 예로 들 수 있습니다.

  • 구현 코드

      array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

  for i in range(1, len(array)):      # 각 데이터 확인
      for j in range(i, 0, -1):       # 인덱스 i부터 1까지 1씩 감소하며 반복하는 문법
          if array[j] < array[j - 1]: # 한 칸씩 왼쪽으로 이동
              array[j], array[j - 1] = array[j - 1], array[j]
          else:                       # 자기보다 작은 데이터를 만나면 그 위치에서 멈춤
              break

  print(array)

버블 정렬

  • 개념

    • 반복적으로 인접한 두 개의 데이터를 비교하며 교환하는 알고리즘입니다.

  • 특징

    • 각 반복이 끝날때마다 가장 큰 값이 가장 오른쪽에 위치하게 됩니다. (오름차순 정렬일 경우)
    • 시간복잡도는 현재 데이터의 정렬 상태와 상관이 없습니다.

  • 시간복잡도

    • 항상 O(N^2)

  • 구현코드

      array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

  for i in range(len(array)-1, 0, -1):        # 정렬 범위 줄이기
      for j in range(i):                      # 인접한 값들의 대소 비교
          if (array[j] > array[j+1]):
              array[j], array[j+1] = array[j+1], array[j]

  print(array)

병합 정렬

  • 개념

    • 주어진 배열을 원소가 하나만 남을때까지 반으로 나눈 뒤(divide),
    • 나눠진 부분 집합의 원소들을 정렬하고(conquer)
    • 정렬된 부분 집합들을 하나의 집합으로 결합(combine)하는 알고리즘입니다.

  • 특징

    • 시간복잡도는 현재 데이터의 정렬 상태와 상관이 없습니다.

  • 시간복잡도

    • 항상 O(NlogN)

  • 구현코드

      array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

  def merge_sort(array):
    if len(array) < 2:
      return array

    mid = len(array) // 2
    left = merge_sort(array[:mid])
    right = merge_sort(array[mid:]) 
    return merge(left, right)

  def merge(left, right):
      result = []
      i = j = 0
      while i < len(left) and j < len(right): # 둘 중 하나가 끝날 때까지
        if left[i] <= right[j]:
          result.append(left[i])
          i += 1
        else:
          result.append(right[j])
          j += 1

      if i == len(left):      # 왼쪽 배열이 끝났다면 오른쪽 배열의 나머지 모두 담음
        result += right[j:]

      else:                   # 오른쪽 배열이 끝났다면 왼쪽 배열의 나머지 모두 담음
        result += left[i:]

      return result

  array = merge_sort(array)
  print(array)

힙 정렬

  • 개념

    • 힙 속성을 만족하도록 트리를 구성함으로써 데이터를 정렬하는 알고리즘입니다.
    • 힙 속성이란, 부모 노드의 값이 자식노드의 값보다 크거나 작은 속성을 의미합니다.
    • 최대 힙 트리로는 내림차순 정렬을, 최소 힙 트리로는 오름차순 정렬을 할 수 있습니다.

  • 특징

    • 시간복잡도는 현재 데이터의 정렬 상태와 상관이 없습니다.

  • 시간복잡도

    • 항상 O(NlogN)

  • 구현코드 ( 최소힙 )

      array = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]

  # 1. 상향식: 특정 노드를 기준으로 위로 올라감
  def heap_sort(array):
      n = len(array)
      # heap 구성
      for i in range(n):
          c = i
          while c != 0:
              r = (c-1)//2
              if (array[r] < array[c]):
                  array[r], array[c] = array[c], array[r]
              c = r
              print(array)
      # 크기를 줄여가면서 heap 구성
      for j in range(n-1, -1, -1):
          array[0] , array[j] = array[j], array[0]
          r = 0
          c = 1
          while c<j:
              c = 2*r +1
              # 자식 중 더 큰 값 찾기
              if (c<j-1) and (array[c] < array[c+1]):
                  c += 1
              # 루트보다 자식이 크다면 교환
              if (c<j) and (array[r] < array[c]):
                  array[r], array[c] = array[c], array[r]
              r=c
              print(array)
      print(array)
  heap_sort(array)

퀵 정렬

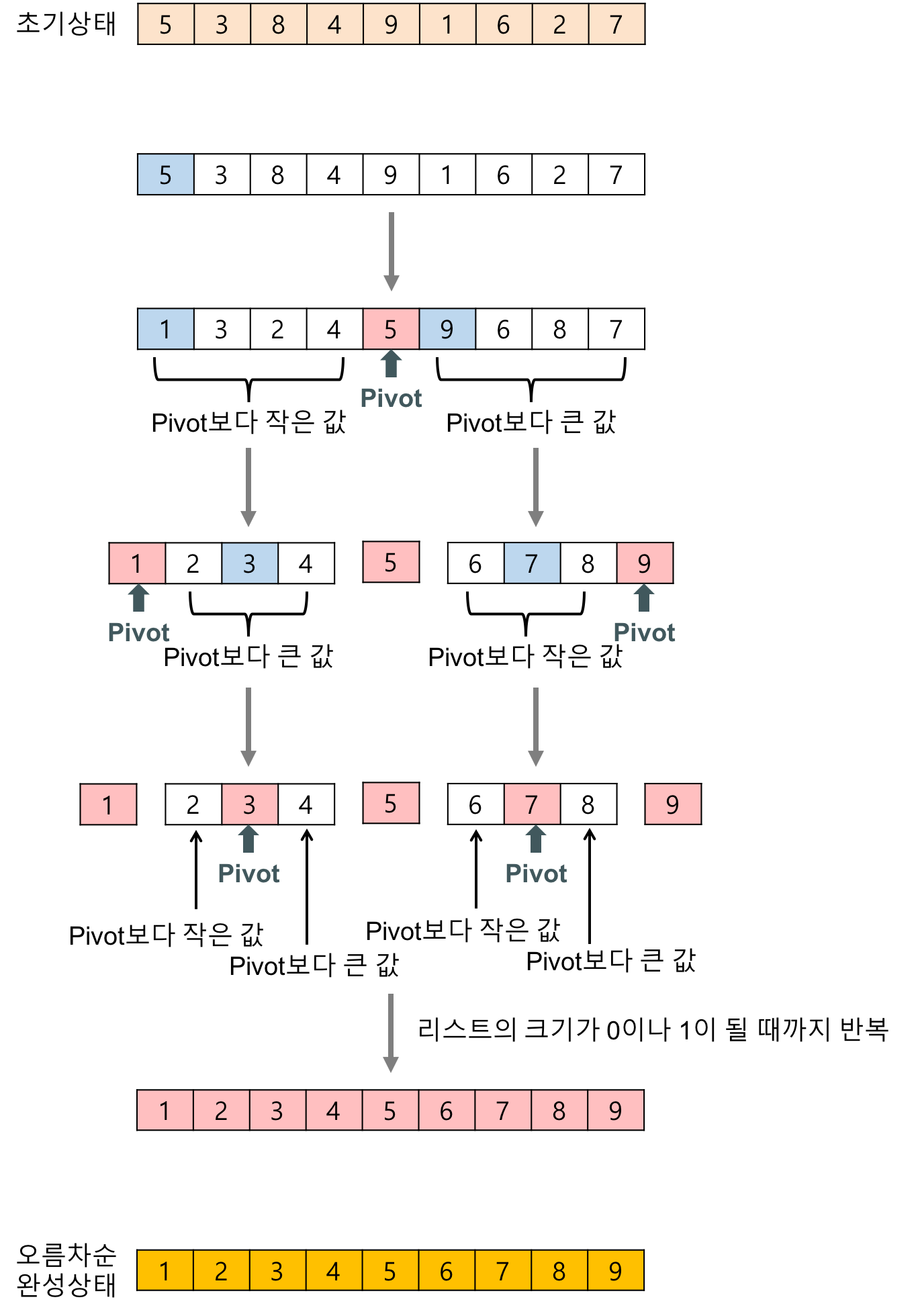
  • 개념

    • 퀵정렬도 분할정복을 사용한 정렬 알고리즘입니다.
    • 먼저, 기준 데이터를 설정하고,
    • 정렬 되지 않은 데이터들을 탐색하며, 기준 데이터보다 큰 데이터와 작은 데이터들의 위치를 바꾸는 과정을 반복합니다.
    • 만약, 큰 데이터의 위치와 작은 데이터의 위치가 엇갈릴 경우,
    • 작은 데이터의 위치와 기준 데이터의 위치를 서로 교환한 뒤, 리스트를 반으로 나누는 방식응로 진행되는 알고리즘입니다.

  • 세부 수행 순서

    1. 리스트에서 하나의 원소를 고릅니다. 이 원소를 피벗이라고 부릅니다.
    2. 피벗을 제외한 나머지 데이터들 중에서, 왼쪽부터는 피벗보다 큰 데이터를 찾고, 오른쪽부터는 피벗보다 작은 데이터를 찾습니다.
    3. 큰 데이터와 작은 데이터의 위치를 교환하며, 큰 데이터의 위치와 작은 데이터의 위치가 엇갈릴때까지 해당 과정을 반복합니다.
    4. 피벗보다 큰 데이터의 위치와 작은 데이터의 위치가 엇갈린 경우엔, ‘작은 데이터’의 위치와 ‘피벗’의 위치를 교환합니다. 이 작업을 분할이라고 합니다.
    5. 피벗이 이동한 상태에선, 피벗의 왼쪽에 있는 데이터들은 모두 피벗보다 작고, 피벗의 오른쪽에 있는 데이터들은 모두 피벗보다 크게 됩니다.
    6. 이제 왼쪽 리스트와 오른쪽 리스트 각각에서도 피벗을 설정하여 퀵 정렬을 진행합니다.
    7. 분할된 리스트의 데이터 개수가 1개인 경우엔 해당 리스트에 대한 정렬을 종료합니다.

  • 특징

    • 병합정렬은 분할 단계에서는 아무것도 하지않고, 병합하는 단계에서 정렬을 수행하지만,
    • 퀵정렬은 분할 단계에서 정렬을 수행하고, 병합 단계에서는 아무것도 하지 않습니다.

  • 시간복잡도

    • Best : O(NlogN)
      • 피벗의 위치가 변경되며 분할이 일어날 때마다, 정확히 왼쪽 리스트와 오른쪽 리스트가 절반씩 분할되는 경우
    • Worst : O(N^2)
      • 리스트의 가장 왼쪽 데이터를 피벗으로 삼을 때, 이미 데이터가 정렬되어 있어, 피봇의 위치가 변경되지 않는 경우

  • 구현코드

      array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]

  def quick_sort(array):

          # 리스트가 하나 이하의 원소만을 담고 있다면 종료
      if len(array) <= 1:
          return array

      pivot = array[0] # 피벗은 첫 번째 원소
      tail = array[1:] # 피벗을 제외한 리스트

      left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분
      right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분

      # 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체 리스트를 반환
      return quick_sort(left_side) + [pivot] + quick_sort(right_side)

  print(quick_sort(array))

계수 정렬

  • 개념

    • 가장 작은 데이터와 가장 큰 데이터의 범위을 모두 담을 수 있는 하나의 리스트를 생성한 뒤,
    • 정렬하고자 하는 데이터들을 하나씩 확인하며,
    • 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가시키는 알고리즘입니다.

  • 특징

    • 데이터의 크기가 제한되어, 정수 형태로 표현할 수 있을때만 사용할 수 있습니다.
    • 데이터의 모든 범위를 담을 수 있는 크기의 리스트를 선언해야하기 때문에, 일반적으로 가장 작은 데이터와 가장 큰 데이터의 차이가 1,000,000 을 넘지 않을 때 효과적으로 사용할 수 있습니다.
    • 동일한 값을 가지는 데이터가 여러 개 등장할 때 적합합니다.

  • 시간복잡도

    • 항상 O(N)
      • 모든 데이터가 양의 정수인 상황에서
      • 데이터의 개수를 N, 데이터들 중 최대값을 K라고 할 때,
      • 계수 정렬의 시간 복잡도는 O(N+K) 입니다.
      • 앞에서부터 데이터를 하나씩 확인하며, 리스트에서 적절한 인덱스의 값을 1씩 증가시킬 뿐만 아니라,
      • 추후에 리스트의 각 인덱스 값들을 뽑아내는 과정을, 데이터들 중 최댓값의 크기만큼 반복해야하기 때문입니다.

  • 공간 복잡도

    • 예를 들어, 데이터가 2개(0과 999,999)만 존재한다면, 이럴 때에도 리스트의 크기가 100만 개가 되도록 선언해야합니다.
    • 따라서, 항상 사용할 수 있는 정렬 알고리즘은 아닙니다.

  • 구현코드

      # 모든 원소의 값이 0보다 크거나 같다고 가정
  array = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]
  # 모든 범위를 포함하는 리스트 선언 (모든 값은 0으로 초기화)
  count = [0] * (max(array) + 1)

  for i in range(len(array)):
      count[array[i]] += 1 # 각 데이터에 해당하는 인덱스의 값 증가

  for i in range(len(count)): # 리스트에 기록된 정렬 정보 확인
      for j in range(count[i]):
          print(i, end=' ') # 띄어쓰기를 구분으로 등장한 횟수만큼 인덱스 출력

시간 복잡도 정리

결론

  • 코딩 문제에서, 별도의 요구사항 없이 단순히 정렬을 해야한다면, 기본 정렬 라이브러리를 사용하면 됩니다.
  • 하지만, 데이터의 범위가 한정되어 있거나, 퀵 정렬 기반의 방식보다 더 빠르게 동작해야하는 경우엔, 계수 정렬을 사용하는게 좋습니다.

참고

'Algorithm > Concept' 카테고리의 다른 글

[Algorithm] 플로이드 워셜(Floyd-Warshall) 알고리즘이란?  (0) 2022.07.04
[Algorithm] Top-Down, Bottom-Up 이란?  (0) 2022.06.12
[Algorithm] DFS 와 BFS 문제 구분 방법  (0) 2022.06.05
[Algorithm] DFS 와 BFS 의 동작 과정 간단 비교  (0) 2022.06.05
[Algorithm] N 의 범위에 따른 시간 복잡도 선택  (0) 2022.05.27
'Algorithm/Concept' Related Articles more
Comments