우노
[DP] 백준 7579번 “앱” Python 풀이 본문
문제 링크
풀이
0-1 냅색(배낭) 문제이며, 0-1 냅색 알고리즘의 개념을 알고 있다면 문제에 대해 더 쉽게 이해할 수 있습니다.
문제의 목표
- 특정 메모리를 넘는 최소 비용을 찾는 것
DP 테이블이 의미하는 것
- 0~i 까지의 앱을 종료하거나 종료하지 않았을 때,
- j 만큼의 cost를 사용함으로써 확보 가능한 최대 메모리값
아래 알고리즘을 진행합니다.
- 행은 앱의 개수만큼, 열은 cost의 총 비용만큼 만들어줍니다.
- 행을 차례대로 돌며 아래 알고리즘을 차례대로 수행합니다.
- j cost보다 현재 앱의 cost가 크다면, 아직 앱이 종료되지 않았으므로, 최대 메모리가 갱신되지 않습니다.
- dp[i][j] = dp[i-1][j]
- j cost보다 현재 앱의 cost가 크거나 같다면, 이제 j cost로 확보 가능한 최대 메모리 값을 갱신할 수 있습니다.
- dp[i][j] = max( dp[ i - 1 ][ j - now_cost ] + now_memory, dp[ i - 1 ][ j ] )
- dp[ i - 1 ][ j - now_cost ] + now_memory : 현재 앱을 종료할 때 얻을 수 있는 최대 메모리
- dp[ i - 1 ][ j ] : 현재 앱을 종료하지 않을 때의 기존 최대 메모리
- dp[i][j] = max( dp[ i - 1 ][ j - now_cost ] + now_memory, dp[ i - 1 ][ j ] )
- j cost보다 현재 앱의 cost가 크다면, 아직 앱이 종료되지 않았으므로, 최대 메모리가 갱신되지 않습니다.
- 만약, 현재 dp[i][j]의 값이 필요한 메모리 M 이상이 된다면, 해당 j cost와 이전 j cost를 비교해, 더 작은 cost 값을 사용합니다.
- result = min(result, j)
최종적으로, 아래와 같은 DP 테이블이 완성됩니다.
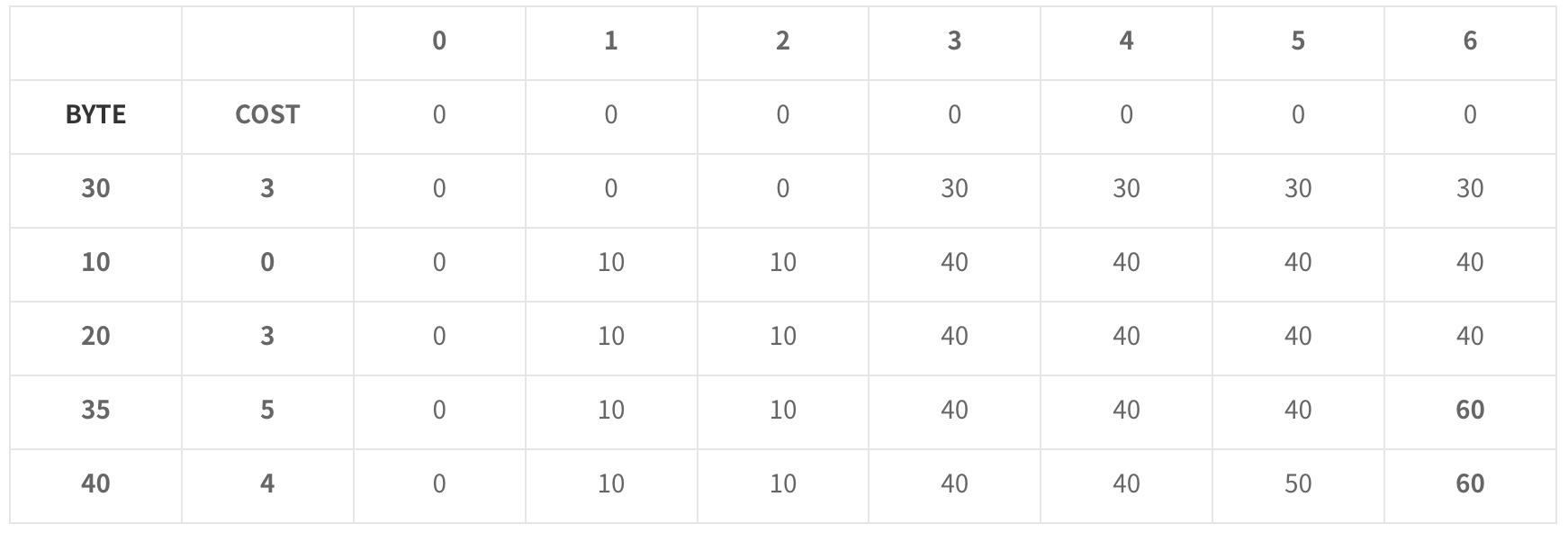
코드
import sys
# 정수의 개수 n과 필요한 메모리 m
n, m = map(int, sys.stdin.readline().split())
# 정수 배열
memory = [0] + list(map(int, sys.stdin.readline().split()))
# 비용 배열
cost = [0] + list(map(int, sys.stdin.readline().split()))
# DP 테이블
# 0~i 까지의 앱을 종료하거나 종료하지 않았을 때,
# j 만큼의 cost를 사용함으로써 확보 가능한 최대 메모리값
dp = [[0] * (sum(cost) + 1) for _ in range(n+1)]
# 필요한 메모리를 확보할 수 있는 최소 비용
result = int(1e9)
# DP 테이블 탐색 시작
# 아이템의 개수 + 1 만큼
for i in range(1, n+1):
# 총 비용의 합 + 1 만큼
for j in range(sum(cost)+1):
# 현재 아이템의 메모리
now_memory = memory[i]
# 현재 아이템의 비용
now_cost = cost[i]
# j cost보다 현재 앱의 cost가 크다면, 아직 앱이 종료되지 않았으므로, 최대 메모리가 갱신되지 않습니다.
if (j < cost[i]):
dp[i][j] = dp[i-1][j]
# j cost보다 현재 앱의 cost가 크거나 같다면, 이제 j cost로 확보 가능한 최대 메모리 값을 갱신할 수 있습니다.
else:
dp[i][j] = max(dp[i-1][j-now_cost] + now_memory, dp[i-1][j])
# 현재 dp[i][j]의 값이 필요한 메모리 M 이상이 된다면
if (dp[i][j] >= m):
# 해당 j cost와 이전 j cost를 비교해, 더 작은 cost 값을 사용합니다.
result = min(result, j)
print(result)참고
'Algorithm > Dynamic Programming' 카테고리의 다른 글
| [DP] 백준 2169번 “로봇 조종하기” Python 풀이 (1) | 2022.10.13 |
|---|---|
| [DP] 백준 5582번 “공통 부분 문자열” Python 풀이 (0) | 2022.10.13 |
| [DP] 백준 10942번 “팰린드롬?” Python 풀이 (1) | 2022.10.12 |
| [DP] 백준 10164번 “격자상의 경로” Python 풀이 (0) | 2022.10.12 |
| [DP] 백준 11726번 “2xn 타일링” Python 풀이 (0) | 2022.10.10 |
Comments




