우노
[ML] 의사결정트리(Decision Tree) 란? 본문
의사결정트리(Decision Tree)란?
- 의사결정트리는 일련의 분류 규칙을 통해 데이터를 분류, 회귀하는 지도 학습 모델 중 하나이며,
- 결과 모델이 Tree 구조를 가지고 있기 때문에 Decision Tree라는 이름을 가집니다.
- 아래 그림을 보면 더 쉽게 이해가 가능합니다.

- 위 그림은 대표적인 의사결정트리의 예시로서, 타이타닉호의 탑승객의 생존여부를 나타내고 있습니다.
- 이렇게 특정 기준(질문)에 따라 데이터를 구분하는 모델을 의사 결정 트리 모델이라고 합니다.
- 한번의 분기 때마다 변수 영역을 두 개로 구분합니다.
- 결정 트리에서 질문이나 정답은 노드(Node)라고 불립니다.
- 맨 처음 분류 기준을 Root Node라고 하고
- 중간 분류 기준을 Intermediate Node
- 맨 마지막 노드를 Terminal Node 혹은 Leaf Node라고 합니다.
- 결정 트리의 기본 아이디어는, Leaf Node가 가장 섞이지 않은 상태로 완전히 분류되는 것, 즉 복잡성(entropy)이 낮도록 만드는 것입니다.
불순도 (Impurity)
- 위의 그림처럼 결정트리에서 분기기준을 선택하기 위해서는 불순도(impurity)라는 개념을 사용합니다.
- 복잡성을 의미하며, 해당 범주 안에 서로 다른 데이터가 얼마나 섞여 있는지를 뜻합니다.
- 다양한 개체들이 섞여 있을수록 불순도가 높아집니다.
- 분기기준 설정 시 현재노드의 불순도에 비해 자식노드의 불순도가 감소되도록 설정해야하며
- 현재 노드의 불순도와 자식노드의 불순도 차이를 Information Gain(정보 획득)이라고 합니다.
불순도 함수 (Gini, Entropy)
불순도를 수치적으로 나타낼 수 있는 대표적인 불순도 함수는 두가지가 있습니다.
지니 지수(Gini)
공식

- 지니 지수의 최대값은 0.5이다.
범주 안에 빨간색 점 10개, 파란색 점이 6개 있을 때의 계산 예제입니다.

엔트로피 지수(Entropy)
공식

범주 안에 빨간색 점 10개, 파란색 점이 6개 있을 때의 계산 예제입니다.

- 분기를 하였을때 이러한 불순도 함수의 값(지니 지수 또는 엔트로피 지수)이 줄어드는 방향으로 트리를 형성해야합니다.
정보획득 (Information gain)
분기 이전의 불순도와 분기 이후의 불순도의 차이를 정보 획득이라고 합니다.
불순도가 1인 상태에서 0.7인 상태로 바뀌었다면 정보 획득(information gain)은 0.3입니다.
자세한 결정트리 구성 단계는 다음과 같습니다.
- Root 노드의 불순도 계산
- 나머지 속성에 대해 분할 후 자식노드의 불순도 계산
- 각 속성에 대한 Information Gain 계산 후 Information Gain(Root노드와 자식노드의 불순도 차이)이 최대가 되는 분기조건을 찾아 분기
- 모든 leaf 노드의 불순도가 0이 될때까지 2,3을 반복 수행한다.
예제) 테니스 경기 참가 여부

Approach 1) Root 노드의 불순도 계산

Approach 2) 나머지 속성에 대해 분할 후 자식노드의 불순도 계산
2-1) 날씨

2-2) 온도

2-3) 습도

2-4) 바람
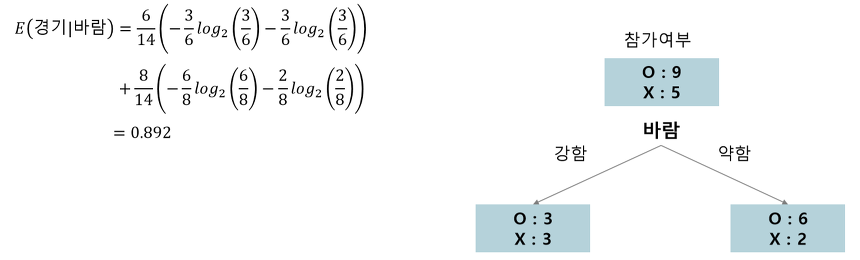
Approach 3) 각 속성에 대한 Information Gain 계산 후 Information Gain(Root노드와 자식노드의 불순도 차이)이 최대가 되는 분기조건을 찾아 분기

Approach 4) 모든 leaf 노드의 불순도가 0이 될때까지 2,3을 반복 수행한다.
예를 들어, "맑음"으로 분류된 노드는 "날씨 = 맑음" 인 데이터만 가지고 와서 다시 분할 전 엔트로피를 계산한다.



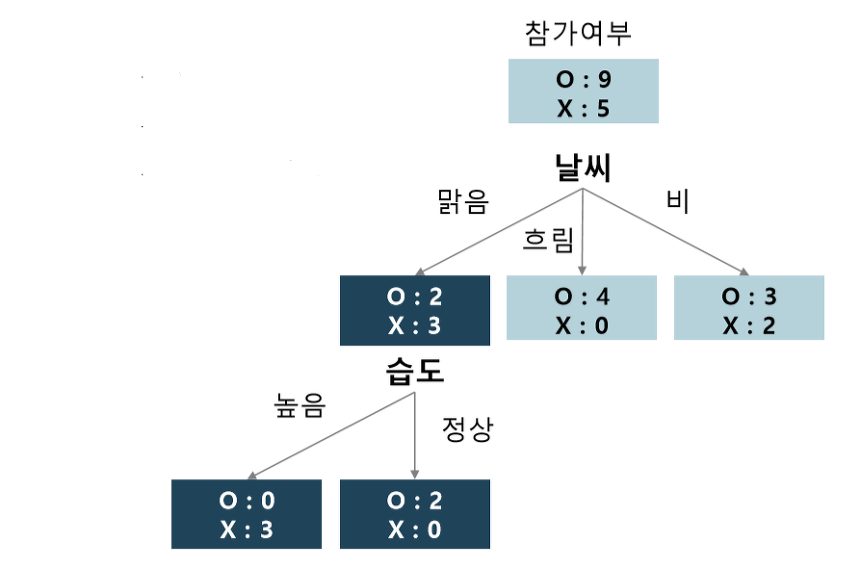
최종결과

일반화
- 위 구성방법을 사용하여 트리를 형성하게 되면, leaf 노드가 순도 100%의 한가지 범주만을 가지게 되는 Full tree(최대 트리)를 형성하게 된다.
- 하지만 이러한 최대 트리는 새로운 데이터에 적용할 때 과적합 문제(Overfitting)가 발생하여 일반화 성능이 떨어지게 된다.
- 따라서 형성된 결정트리에 대해 가지치기(Pruning)를 수행하여 일반화 성능을 높힌다.
가지치기 (pruning)

- 가지치기란 최대트리로 형성된 결정트리의 특정 노드 밑의 하부 트리를 제거하여 일반화 성능을 높히는 것을 의미한다. (오버피팅을 막기위해 사용된다.)
- 더 많은 가지가 생기지 않도록 최대 깊이, leaf 노드의 최대 개수, 한 노드가 분할하기 위한 최소 데이터 수 등의 제한이 가능하다.
가지치기의 비용함수
- 의사결정나무는 이 비용함수를 최소로 하는 분기를 찾아내도록 학습됩니다. 아래와 같이 정의됩니다.
- CC(T) = Err(T) + α × L(T)
- CC(T)
- 의사결정나무의 비용 복잡도
- 오류가 적으면서 terminal node 수가 적은 단순한 모델일 수록 작은 값
- ERR(T)
- 검증데이터에 대한 오분류율
- L(T)
- terminal node의 수
- 구조의 복잡도
- Alpha
- ERR(T)와 L(T)를 결합하는 가중치
- 사용자에 의해 부여됨, 보통 0.01~0.1의 값을 씀
- CC(T)
장점
- 데이터의 전처리 (정규화, 결측치, 이상치 등) 를 하지 않아도 된다.
- 수치형과 범주형 변수를 한꺼번에 다룰 수 있다.
한계
- 만약 샘플의 사이즈가 크면 효율성 및 가독성이 떨어진다.
- 과적합으로 알고리즘 성능이 떨어질 수 있다.
- 이를 극복하기 위해서 트리의 크기를 사전에 제한하는 튜닝이 필요하다.
- 한 번에 하나의 변수만을 고려하므로 변수간 상호작용을 파악하기가 어렵다.
- 결정트리는 Hill Climbing 방식 및 Greedy 방식을 사용하고 있다.
- 일반적인 Greedy 방식의 알고리즘이 그렇듯이 이 방식은 최적의 해를 보장하지는 못한다.
- 약간의 차이에 따라 (레코드의 개수의 약간의 차이) 트리의 모양이 많이 달라질 수 있다.
- 두 변수가 비슷한 수준의 정보력을 갖는다고 했을 때, 약간의 차이에 의해 다른 변수가 선택되면 이 후의 트리 구성이 크게 달라질 수 있다.
- 이같은 문제를 극복하기 위해 등장한 모델이 바로 랜덤포레스트이다.
- 같은 데이터에 대해 의사결정나무를 여러 개 만들어 그 결과를 종합해 예측 성능을 높이는 기법이다.
'AI > Machine Learning' 카테고리의 다른 글
| [ML] NNLS(Non-negative least squares)란? (0) | 2020.09.07 |
|---|---|
| [ML] 교차검증 (CV, Cross Validation) 이란? (8) | 2020.08.14 |
| [ML] Data Preprocessing - Missing Value (결측치 처리) (0) | 2020.08.11 |
| [ML] 베이지안 최적화 (Bayesian Optimization) (29) | 2020.08.10 |
| [ML] 이상값(outlier)과 로버스트(robust) (2) | 2020.08.06 |
Comments



