우노
[ML] 베이지안 최적화 (Bayesian Optimization) 본문
- Hyperparameter Optimization이란, 학습을 수행하기 위해 사전에 설정해야 하는 값인 hyperparameter(하이퍼파라미터)의 최적값을 탐색하는 문제를 지칭합니다.
- 보통 Hyperparameter를 찾기 위해 사용되는 방법으로는 Manual Search, Grid Search, Random Search, Bayesian optimization, Evolutionary algorithm 등이 있습니다.
- 여기서 다룰 내용은 Manual Search, Grid Search, Random Search, Bayesian optimization입니다.
Manual Search
- 여러분들은 보통 직관 또는 대중적으로 알려진 노하우 등에 의존하여, hyperparameter 값을 선정하고, 이들을 사용하여 학습을 수행한 후 검증 데이터셋(validation set)에 대하여 측정한 성능 결과를 기록합니다.
- 이러한 과정을 몇 차례 거듭한 후, 맨 마지막 시점까지의 시도들 중 검증 데이터셋에 대하여 가장 높은 성능을 발휘했던 hyperparameter 값을 채택해 왔을 것입니다.
- 이와 같이 최적 hyperparameter 값을 직접 탐색하는 방법을 Manual Search라고도 합니다.
- 하지만 여러분들이 찾은 최적의 hyperparameter 값이 ‘실제로도’ 최적이라는 사실을 보장하기가 상대적으로 어렵다는 단점이 있습니다.
- 또한 한 번에 여러 종류의 hyperparameter들을 탐색하고자 할 시, 문제가 더욱 복잡해진다는 것입니다.
- 여러 종류의 hyperparameter들 중에는, 서로 간의 상호 영향 관계를 나타내는 것들도 존재하기 때문에
- 둘 이상의 hyperparameter들에 대한 탐색을 한 번에 진행할 시, 단일 hyperparameter 각각에 대하여 기존의 직관을 적용하기가 매우 어려워집니다.
Grid Search
- Manual Search에 비해, Grid Search와 Random Search는 체계적인 방식으로 Hyperparameter Optimization을 수행합니다.
- Grid Search는 탐색의 대상이 되는 특정 구간 내의 후보 hyperparameter 값들을 일정한 간격을 두고 선정하여, 이들 각각에 대하여 측정한 성능 결과를 기록한 뒤, 가장 높은 성능을 발휘했던 hyperparameter 값을 선정하는 방법입니다.
- 즉, 모든 parameter의 경우의 수에 대해 cross-validation 결과가 가장 좋은 parameter를 고르는 방법이다.
- 전체 탐색 대상 구간을 어떻게 설정할지, 간격은 어떻게 설정할지 등을 결정하는 데 있어 여전히 사람의 손이 필요하나
- 앞선 Manual Search와 비교하면 좀 더 균등하고 전역적인 탐색이 가능하다는 장점이 있습니다.
- 하지만 탐색하고자하는 hyperparameter의 개수를 한 번에 여러 종류로 가져갈수록, 전체 탐색 시간이 기하급수적으로 증가한다는 단점이 있습니다.
Random Search
- Random Search는 Grid Search와 큰 맥락은 유사하나
- 탐색 대상 구간 내의 후보 hyperparameter 값들을 랜덤 샘플링(sampling)을 통해 선정한다는 점이 다릅니다.
- Random Search는 Grid Search에 비해 불필요한 반복 수행 횟수를 대폭 줄이면서, 동시에 정해진 간격(grid) 사이에 위치한 값들에 대해서도 확률적으로 탐색이 가능하므로, 최적 hyperparameter 값을 더 빨리 찾을 수 있는 것으로 알려져 있습니다.
- 즉, Random Search는 모든 grid를 전부 search 하는 대신, random하게 일부의 parameter 들만 관측한 후, 그 중에서 가장 좋은 parameter를 고릅니다.
- Grid Search는 Unimportant parameter와 Important Parameter를 동일하게 관측해야하기 때문에, 정작 Important Parameter를 다양하게 시도해볼 수 있는 기회가 적지만
- Random Search는 grid로 제한되지 않기 때문에 확률적으로 Important Parameter를 더 살펴볼 수 있는 기회를 받게 됩니다.
- 그럼에도 불구하고, Random Search에서도 '여전히 약간의 불필요한 탐색을 반복하는 것 같다’는 느낌을 지우기 어려우실 것이라고 생각합니다.
- 왜냐하면 Grid Search와 Random Search 모두, 바로 다음 번 시도할 후보 hyperparameter 값을 선정하는 과정에서, 이전까지의 조사 과정에서 얻어진 hyperparameter 값들의 성능 결과에 대한 ‘사전 지식’이 전혀 반영되어 있지 않기 때문입니다.
- 매 회 새로운 hyperparameter 값에 대한 조사를 수행할 시 ‘사전 지식’을 충분히 반영하면서, 동시에 전체적인 탐색 과정을 체계적으로 수행할 수 있는 방법론으로, Bayesian Optimization을 들 수 있습니다.
Bayesian optimization
Bayesian Optimization 은 어느 입력값(x)를 받는 미지의 목적 함수(f(x))를 상정하여,
해당 함숫값(f(x))을 최대로 만드는 최적해를 찾는 것을 목적으로 합니다.
- 즉, 목적 함수(탐색대상함수)와 하이퍼파라미터 쌍(pair)을 대상으로 Surrogate Model(대체 모델) 을 만들고,
- 순차적으로 하이퍼 파라미터를 업데이트해 가면서 평가를 통해 최적의 하이퍼파라미터 조합을 탐색합니다.
- 이 때의 목점 함수를 black-box function 이라고 합니다.
Bayesian Optimization 에는 두 가지 필수 요소가 존재합니다.
- 먼저 Surrogate Model 은, 현재까지 조사된 입력값-함숫결과값 점들 (x1, f(x1)),...,(xt, f(xt)) 을 바탕으로, 미지의 목적 함수의 형태에 대한 확률적인 추정을 수행하는 모델을 지칭합니다.
- 그리고 Acquisition Function 은, 목적 함수에 대한 현재까지의 확률적 추정 결과를 바탕으로, ‘최적 입력값을 찾는 데 있어 가장 유용할 만한’ 다음 입력값 후보를 추천해 주는 함수를 지칭합니다.
Bayesian Optimization 수행 과정
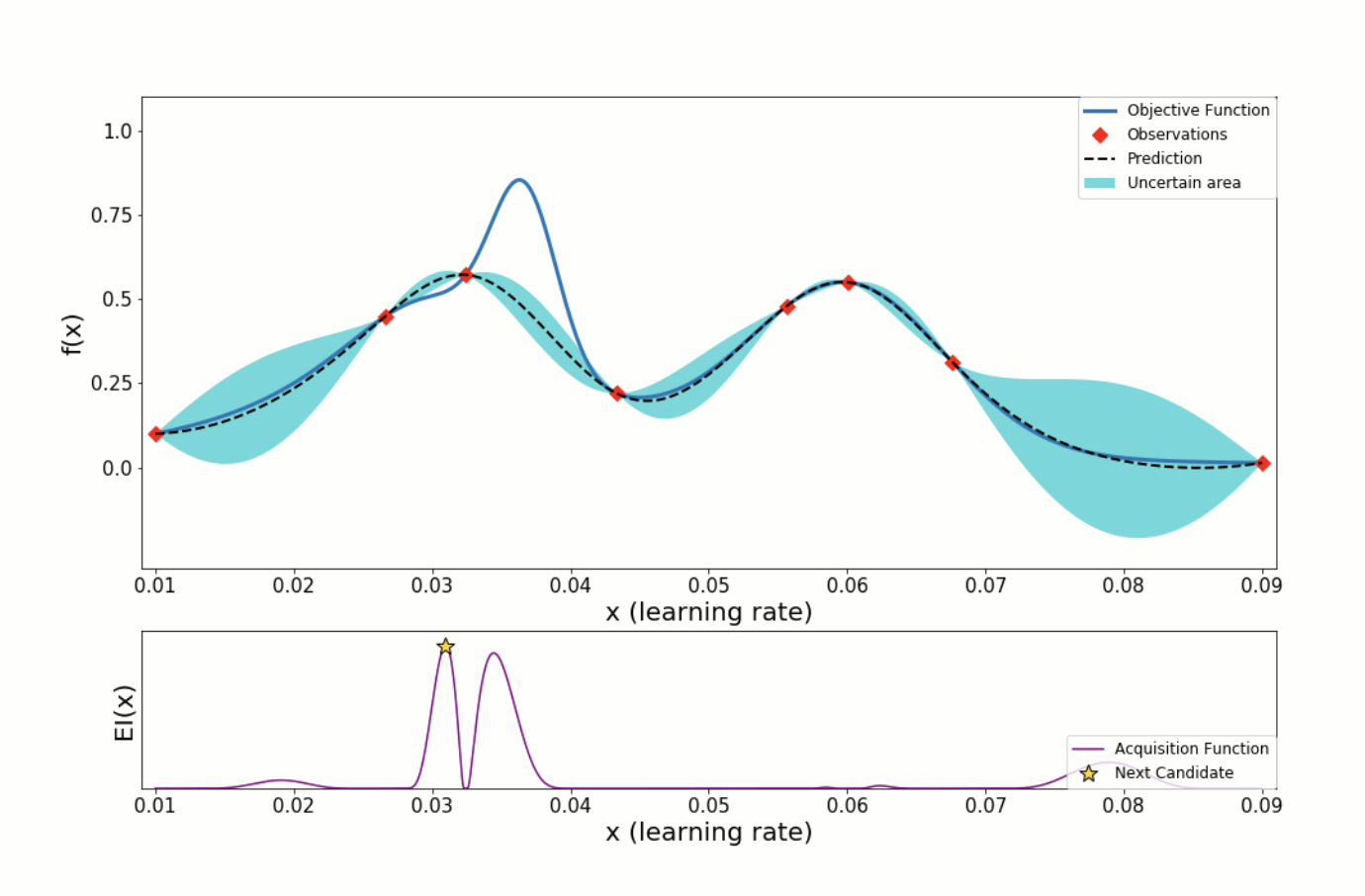
대략적인 수행 과정
- 위의 파란색 선은, 우리가 찾으려고 하는 목적함수 f(x) 를 나타내고,
- 검정색 점선은, 지금까지 관측한 데이터를 바탕으로 우리가 예측한 estimated function 을 의미합니다.
- 검정색 점선 주변에 있는 파란 영역은, 목적함수 f(x) 가 존재할만한 confidence bound(function의 variance) 를 의미합니다.
- 밑에 있는 EI(x) 는, Acquisition function 을 의미하며, 다음 입력값 후보 추천 시 사용됩니다.
- Acquisition function 값이 컸던 지점을 확인하고, 해당 지점의 hyperparameter 를 다음 입력 값으로 사용합니다.
- hyperparamter 에 따라 estimated function 을 계속 update 하면, estimation function 과 목적 함수 f(x) 가 흡사해집니다.
- 관측한 지점 중 best point 을 argmax f(x) 로 선택합니다.
자세한 수행 과정
입력값, 목적 함수 및 그 외 설정값들을 정의합니다.
- 입력값 x : 여러가지 hyperparameter
- 목적 함수 f(x) : 설정한 입력값을 적용해 학습한, 딥러닝 모델의 성능 결과 수치(e.g. 정확도)
- 입력값 x 의 탐색 대상 구간 : (a,b)
- 입력값-함숫결과값 점들의 갯수 : n
- 조사할 입력값-함숫결과값 점들의 갯수 : N
설정한 탐색 대상 구간 (a,b) 내에서 처음 n 개의 입력값들을 랜덤하게 샘플링하여 선택합니다.
선택한 n 개의 입력값 x1, x2, ..., xn 을 각각 모델의 hyperparameter 로 설정하여 딥러닝 모델을 학습한 뒤, 학습이 완료된 모델의 성능 결과 수치를 계산합니다.
- 이들을 각각 함숫결과값 f(x1), f(x2), ..., f(xn) 으로 간주합니다.
입력값-함숫결과값 점들의 모음 (x1, f(x1)), (x2, f(x2)), ..., (xn, f(xn)) 에 대하여 Surrogate Model 로 확률적 추정을 수행합니다.
조사된 입력값-함숫결과값 점들이 총 N 개에 도달할 때까지, 아래의 과정을 반복적으로 수행합니다.
- 기존 입력값-함숫결과값 점들의 모음 (x1, f(x1)),(x2, f(x2)), ..., (xt, f(xt)) 에 대한 Surrogate Model 의 확률적 추정 결과를 바탕으로, 입력값 구간 (a,b) 내에서의 EI 의 값을 계산하고, 그 값이 가장 큰 점을 다음 입력값 후보 x1 로 선정합니다.
- 다음 입력값 후보 x1 를 hyperparameter 로 설정하여 딥러닝 모델을 학습한 뒤, 학습이 완료된 모델의 성능 결과 수치를 계산하고, 이를 f(x1) 값으로 간주합니다.
- 새로운 점 (x2, f(x2)) 을 기존 입력값-함숫결과값 점들의 모음에 추가하고, 갱신된 점들의 모음에 대하여 Surrogate Model 로 확률적 추정을 다시 수행합니다.
총 N 개의 입력값-함숫결과값 점들에 대하여 확률적으로 추정된 목적 함수 결과물을 바탕으로, 평균 함수 μ(x) 을 최대로 만드는 최적해를 최종 선택합니다. 추후 해당값을 hyperparameter 로 사용하여 딥러닝 모델을 학습하면, 일반화 성능이 극대화된 모델을 얻을 수 있습니다.
XGBRegressor Bayesian Optimization 예제 코드
XGBoost에서 사용하는 Hyper-parameter로는 다음과 같다.
- max_depth(int, default: 3): 기본 학습자를 위한 최대 트리 깊이
- learning_rate(float, default: 0.1) : Boosting 학습률
- n_estimators(int, default: 100) : fit하기 위한 Boosted tree의 수
- silent(boolean, default: True : Boosting을 실행하는 동안 메시지를 print할지 여부
- objective(string or callable, default:’reg:linear’) : 학습할 Objective Function 사용
- booster(string, default: ‘gbtree’): Booster가 사용할 모드 gbtree, gblinear, dart
- nthread(int, default: ‘None’): xgboost를 실행하는데 사용할 병렬 스레드 수
- n_jobs(int, default: 1): xgboost를 실행하는데 사용할 병렬 스레드 수
- gamma(float, default: 0): 트리의 leaf 노드에 추가 파티션(partition)을 만들때 최소 손실 감소(Minimum loss reduction)가 필요하다.
- min_child_weight(int, default: 1): Child 노드에 필요한 instance weight(hessian) 최소 합계
- max_delta_step(int): 각 Tree의 가중치(Weight) 추정을 허용하는 최대 Delta 단계
- subsample(float): 학습(Training) Instance의 Subsample 비율
- colsample_bytree(float): 각 Tree를 구성할 때 column의 Subsample 비율
- colsample_bylevel(float): 각 Tree의 Level에서 분할(split)에 대한 column의 Subsample 비율
- reg_alpha(float): Weight에 대한 L1 정규화(regularization)
- reg_lambda(float): Weight에 대한 L2 정규화(regularization)
- scales_pos_weight(float): 양의 클래스와 음의 클래스에 대한 균형
- base_score: 모든 Instance의 초기 예측 점수(prediction score)
- seed(int): 난수 (Random) seed값 (random_state를 사용할 것)
- random_state(int): seed와 동일
- missing(float, defualt np.nan): 누락된 값(Missing Value)으로 존재하는 데이터를 처리할 값.
탐색 대상 함수 정의
from sklearn.metrics import r2_score, mean_squared_error import xgboost as xgb # MAPE Metric def mean_absolute_percentage_error(y_test, y_pred): y_test, y_pred = np.array(y_test), np.array(y_pred) return np.mean(np.abs((y_test - y_pred) / y_test)) * 100 # 탐색 대상 함수 (XGBRegressor) def XGB_cv(max_depth,learning_rate, n_estimators, gamma ,min_child_weight, subsample ,colsample_bytree, silent=True, nthread=-1): # 모델 정의 model = xgb.XGBRegressor(max_depth=int(max_depth), learning_rate=learning_rate, n_estimators=int(n_estimators), gamma=gamma, min_child_weight=min_child_weight, subsample=subsample, colsample_bytree=colsample_bytree, nthread=nthread ) # 모델 훈련 model.fit(X_train, y_train) # 예측값 출력 y_pred= model.predict(X_test) # 각종 metric 계산 rmse = np.sqrt(mean_squared_error(y_test, y_pred)) r2 = r2_score(y_test, y_pred) mape = mean_absolute_percentage_error(y_test, y_pred) # 오차 최적화로 사용할 metric 반환 return r2하이퍼파라미터 정의 후 Bayesian optimization 진행
# bayesian-optimization 라이브러리의 BayesianOptimization 클래스 import from bayes_opt import BayesianOptimization import numpy as np # 실험해보고자하는 hyperparameter 집합 pbounds = {'max_depth': (3, 7), 'learning_rate': (0.01, 0.2), 'n_estimators': (5000, 10000), 'gamma': (0, 100), 'min_child_weight': (0, 3), 'subsample': (0.5, 1), 'colsample_bytree' :(0.2, 1) } # Bayesian optimization 객체 생성 # f : 탐색 대상 함수, pbounds : hyperparameter 집합 # verbose = 2 항상 출력, verbose = 1 최댓값일 때 출력, verbose = 0 출력 안함 # random_state : Bayesian Optimization 상의 랜덤성이 존재하는 부분을 통제 bo=BayesianOptimization(f=XGB_cv, pbounds=pbounds, verbose=2, random_state=1 ) # 메소드를 이용해 최대화 과정 수행 # init_points : 초기 Random Search 갯수 # n_iter : 반복 횟수 (몇개의 입력값-함숫값 점들을 확인할지! 많을 수록 정확한 값을 얻을 수 있다.) # acq : Acquisition Function들 중 Expected Improvement(EI) 를 사용 # xi : exploration 강도 (기본값은 0.0) bo.maximize(init_points=2, n_iter=10, acq='ei', xi=0.01) # ‘iter’는 반복 회차, ‘target’은 목적 함수의 값, 나머지는 입력값을 나타냅니다. # 현재 회차 이전까지 조사된 함숫값들과 비교하여, 현재 회차에 최댓값이 얻어진 경우, # bayesian-optimization 라이브러리는 이를 자동으로 다른 색 글자로 표시하는 것을 확인할 수 있습니다 # 찾은 파라미터 값 확인 print(bo.max)
'AI > Machine Learning' 카테고리의 다른 글
| [ML] 의사결정트리(Decision Tree) 란? (11) | 2020.08.13 |
|---|---|
| [ML] Data Preprocessing - Missing Value (결측치 처리) (0) | 2020.08.11 |
| [ML] 이상값(outlier)과 로버스트(robust) (2) | 2020.08.06 |
| [ML] Model compile() - 학습과정 설정 (0) | 2020.08.06 |
| [ML] Metric 종류 (0) | 2020.08.06 |

