우노
[DL] 활성화 함수의 역할 및 종류 본문
활성화 함수의 역할
- 딥러닝 네트워크에서는 노드에 들어오는 값들을 곧바로 다음 레이어로 전달하지 않고, 주로 비선형 함수를 통과시켜 전달한다.
- 이때 사용하는 함수를 활성화 함수(Activation Function)라고 부른다.
- 여기서 주로 비선형 함수를 사용하는 이유는, 선형함수를 사용할 시 층을 깊게 하는 의미가 줄어들기 때문이다.
- 예를 들어, 선형함수 h(x)=cx 를 활성화함수로 사용하는 3-Layer 네트워크가 있다고 가정해보자.
- 해당 네트워크를 식으로 나타내면 y(x)=h(h(h(x))) 가 된다.
- 이는 실은 y(x)=c^3x 와 똑같은 식이기 때문에, 결국 하나의 layer로 깊은 layer를 표현 할 수 있다는 것이다.
- 즉, linear한 연산을 갖는 layer는 수십개 쌓아도, 결국 하나의 linear 연산으로 나타낼 수 있다는 것이다.
- 따라서, 뉴럴네트워크에서 층을 쌓는 혜택을 얻고 싶다면, 활성화함수로는 반드시 비선형 함수를 사용해야 한다.
Sigmoid Function (시그모이드 함수)
기본 수식과 미분 수식

그래프

특징
- 이 함수는 0과 1사이의 값만 가질 수 있도록하는 비선형 함수이다.
- 하지만, 보통 Sigmoid Function은 이진 분류(0, 1) 출력을 가지는 출력층에서만 사용된다.
- 보통 은닉층에서는 사용하지 않는다.
Tanh Functinon (하이퍼볼릭탄젠트 함수)
기본 수식과 미분 수식

그래프

특징
- 이 함수는 -1 ~ 1 사이의 값을 가질 수 있도록 하는 비선형 함수이다.
- 수학적으로는 0 ~ 1 사이의 값을 갖는 Sigmoid Function을 평행이동한 것과 동일하다.
- 데이터 중심을 0으로 위치시키는 효과가 있기 때문에, 다음 층의 학습이 더 쉽게 이루어진다.
- 따라서, 보통 Sigmoid Function보다 더 좋은 성능을 발휘한다.
Sigmoid Function와 Tanh Function의 단점
- Sigmoid Function와 Tanh Function는 한 가지 단점을 가지고 있다.
- 바로, x 가 매우 크거나 매우 작을 때, 함수의 Gradient(미분값,기울기)가 거의 0이 된다는 것이다.
- 따라서, Gradient Vanishing 문제가 발생한다.
- Gradient Vanishing 란 무엇일까?
Gradient Vanishing 정의 및 원인

- Gradient Vanishing 문제란, MLP를 학습시키는 방법인 Backpropagation 중, Gradient 항이 사라지는 문제이다.
- Backpropagation 학습식을 보면 Cost Function의 Gradient 항이 존재한다.
- 이 항이 0이나 0에 가까워져 학습이 불가능해지는 현상을 말하는 것이다.
- 왜 gradient 항이 사라지는 현상이 발생할까?
- 이는 우리가 Activation Function으로 Sigmoid Function을 사용했기 때문이다.
- Sigmoid Function에 대해 자세히 살펴보자.

- Sigmoid Function의 도함수를 살펴보면 최대값이 0.25 인 것을 알 수 있다.
- 다시 말해, Sigmoid Function를 사용한다면 망이 깊어질수록 Gradient가 1/4씩 줄어든다는 의미이다.

- 위 그림은 Backpropagation(역전파) 과정을 수식으로 나타낸것이다.
- W_1의 Gradient를 확인해보면 Backpropagation(역전파)로 인해, Sigmoid의 도함수가 중첩된 것을 볼 수 있다.
- Sigmoid의 도함수는 최대값이 0.25이기 때문에, 결국 Gradient 값이 급격히 줄어들게 된다.
- 이를 해결하기 위해 RELU Function을 사용한다.
RELU Function (렐루 함수)
기본 수식과 미분 수식


그래프

특징
- 이 함수는 x 가 양수면 미분값이 1이고, x 가 음수면 미분값이 0인 함수이다.
- Gradient Vanishing 문제(layer가 늘어날때 값이 사라지는 현상)가 해결되기 떄문에, 가장 기본적인 활성화 함수로 사용된다.
- ReLU 의 한 가지 단점은, x 가 음수일 때 미분값이 0이라는 것이지만, 실제로는 잘 작동한다.
- 하지만 다른 버전의 ReLU 가 있는데, 바로 leaky ReLU 이다.
leaky RELU Function (리키 렐루 함수)
기본 수식

그래프
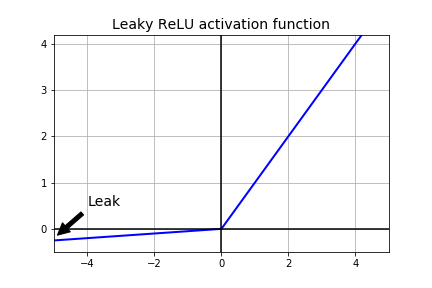
특징
- x가 음수일 때 미분값이 0이 되는 RELU Function 대신, 약간의 기울기를 갖는 함수이다.
- 대개는 ReLU 활성함수 보다 잘 작동하지만 실제로는 잘 사용하지는 않는다.
결론
- Gradient Vanishing 현상은 Activation Function의 변경을 통해 어느정도 보완할 수 있다.
- 하지만, 처음부터 weight 값들이 0 이라면 이 또한 학습이 불가능한 상황이다.
- 따라서, 처음부터 weight 값들을 최적의 값으로 설정한다면 gradient가 작아지더라도, 학습횟수가 적더라도 좋은 모델을 생성할 수 있다.
'AI > Deep Learning' 카테고리의 다른 글
| [DL] 간단한 순전파와 역전파 예제 (5) | 2021.01.12 |
|---|---|
| [DL] 파라미터와 하이퍼파라미터의 차이 (0) | 2021.01.12 |
| [DL] Weight matrix 차원 공식 (0) | 2021.01.11 |
| [DL] 경사 하강법(Gradient Descent) (0) | 2020.07.30 |
| [DL] Keras 단순 선형 회귀 튜토리얼 (0) | 2020.07.29 |
Comments


