우노
[DL] 간단한 순전파와 역전파 예제 본문
순전파(Feedforawrd)와 역전파(Backpropagation)의 개념
- 다층 퍼셉트론으로 학습을 한다는 것은, 최종 출력값과 실제값의 오차가 최소화 되도록 가중치(Weight)와 바이어스(Bias)를 계산하여 결정하는 것입니다.
- 이는, 순전파(Feedforward)를 통해 최종 출력값과 실제값의 오차를 확인하고
- 역전파(Backpropagation)를 통해 최종 출력값과 실제값의 오차가 최소화 되도록 가중치(Weight)와 바이어스(Bias)를 업데이트하며 진행됩니다.
- 예를 들어, 농구에서 자유투를 던지는 과정은 순전파(Feedforward)라고 할 수 있고,
- 던진 공이 어느 지점에 도착했는지를 확인하고 던질 위치를 수정하는 과정을 역전파(Backpropagation)이라고 할 수 있습니다.
예제 : 순전파

예제 신경망을 통해 순전파를 이해해보겠습니다.
Input 값은 1개이고, Output 값은 2개, Hidden Layer 수는 2개인 작은 신경망입니다.
각 노드의 활성화함수는 Sigmoid Function 을 사용했으며, Bias 는 제외하였습니다.
초록색 값들은 처음 주어진 값들이고, 파란색 값들은 초기값을 바탕으로 계산한 값입니다.
처음 x1 의 값은 0.5 이고 W_10(0)은 0.15 이기 때문에, 둘을 곱한 0.075 가 계산 값으로 나온 것을 알 수 있습니다.
결과적으로는, 예측값 y1 은 0.609 이지만, 실제값은 0.3 이고
y2 는 0.633 이지만, 실제값은 0.9 인 것을 확인할 수 있습니다.
따라서, y1 은 감소하는 방향으로 개선해야하고, y2 는 증가하는 방향으로 개선해야 한다는 것을 알 수 있습니다.
Error 측정 방식은 MSE 방식을 사용했고, 전체 Error(E_tot) 는 0.083385 인 것을 알 수 있습니다.

- ((0.3-0.609)^2)/2 + ((0.9-0.633)^2)/2 = 0.083385
가중치 업데이트 공식

- 신경망의 각 가중치는, 위 공식을 통해 업데이트됩니다.
- gradient 는 오차를 해당 가중치로 미분한 값이며, 해당 가중치가 오차에 미치는 영향을 의미합니다.
- 따라서, 오차에 큰 영향을 주는 가중치일수록, gradient 가 커지게 됩니다.
예제 : 역전파 01

역전파 알고리즘을 적용할 때, 신경망의 가중치들은 Output 으로부터 가장 가까운 층부터 계산되며 업데이트 됩니다.
- 업데이트하고자 하는 가중치가 오차에 미치는 영향은,
- 다음층의 가중치가 오차에 미치는 영향을 통해 계산되기 때문입니다.
Output 으로부터 가장 가까운 층에 위치한 가중치는 w_10(1), w_11(1), w_20(1), w_21(1) 이며
아래 그램을 통해, w_10(1) 이 전체 Error(E_tot) 에 미치는 영향부터 계산해보겠습니다.

w_10(1) 이 E_tot 에 미치는 영향은, E_tot 를 w_10(1) 로 미분한 값과 동일하며,
총 3개의 편미분 식으로 나타낼 수 있고, 각 편미분을 계산해, w_10(1) 의 gradient 를 구할 수 있습니다.
w_10(1) 이 E_tot 에 미치는 영향

a_20 이 E_tot 에 미치는 영향

- (0.3 - 0.609) * -1
z_20 이 a_20 에 미치는 영향

- 0.609 * (1 - 0.609)
w_10(1) 이 z_20 에 미치는 영향
z_20 = w_10(1) * a_10 + w_20(1) * a_11

0.518
전체 계산 결과

- 계산 결과, w_10(1) 이 E_tot 에 미치는 영향은 0.0381 이라는 것을 알 수 있습니다.
w_10(1) 의 gradient 를 아래 학습식에 넣어, w_10(1) 을 업데이트 할 수 있습니다.

- 학습률은 0.5 로 지정했습니다.
- 위 결과를 통해, 결과에 영향을 많이 미치는 노드는, 더 많은 오차를 받게 된다는 것을 알 수 있습니다.
위와 같은 방법으로, 나머지 가중치 w_11(1), w_20(1), w_21(1) 가 E_tot 에 미치는 영향을 계산할 수 있으며, 각 가중치를 업데이트 할 수 있습니다.
예제 : 역전파 02
위 예제에서는, Output 으로부터 가장 가까운 층의 가중치들을 업데이트해보았습니다.
해당 예제에서는, Output 으로부터 두 번째 층에 위치한 가중치 w_10(0), w_11(0) 를 업데이트해보겠습니다.
우선, 아래 그림을 통해, w_10(0) 이 전체 Error(E_tot) 에 미치는 영향부터 계산해보겠습니다.

w_10(0) 이 E_tot 에 미치는 영향은, E_tot 를 w_10(0) 로 미분한 값과 동일하며,
총 4개의 편미분 식으로 나타낼 수 있고, 각 편미분을 계산해, w_10(0) 의 gradient 를 구할 수 있습니다.
w_10(0) 이 E_tot 에 미치는 영향



a_10 이 E_1 에 미치는 영향


- 0.0294
a_10 이 E_2 에 미치는 영향


- -0.0328
z_10 이 a_10 에 미치는 영향
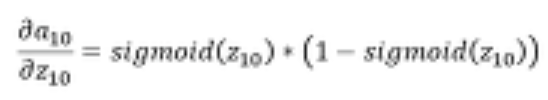
- 0.249
w_10(0) 이 z_10 에 미치는 영향
- z_10 은 x1 * w_10(0) 이므로, w_10(0) 으로 미분하면 x1 만 남는다.
- 0.5
전체 계산 결과

- 계산 결과 w_10(0) 이 E_tot 에 미치는 영향은 -0.00042 라는 것을 알 수 있습니다.
w_10(0) 의 gradient 를 아래 학습식에 넣어, w_10(0) 을 업데이트 할 수 있습니다.

- 학습률은 0.5 로 지정했습니다.
위와 같은 방법으로, 나머지 가중치 w_11(0) 가 E_tot 에 미치는 영향을 계산할 수 있으며, 해당 가중치를 업데이트 할 수 있습니다.
추가
- 위와 같은 역전파를 한 번 돌리는 것을 1 epoch 라고 하며
- epoch 를 늘릴수록 가중치가 계속 업데이트(학습)되면서 오차가 줄어들게 됩니다.
참고
'AI > Deep Learning' 카테고리의 다른 글
| [DL] Bias(편향) vs Variance(분산) (0) | 2021.01.17 |
|---|---|
| [DL] 일반적인 딥러닝 순서 (0) | 2021.01.13 |
| [DL] 파라미터와 하이퍼파라미터의 차이 (0) | 2021.01.12 |
| [DL] Weight matrix 차원 공식 (0) | 2021.01.11 |
| [DL] 활성화 함수의 역할 및 종류 (0) | 2021.01.10 |


