우노
[DP] 이코테 “병사 배치하기” Python 풀이 본문
문제
N명의 병사가 무작위로 나열되어 있다.
각 병사는 특정한 값의 전투력을 보유하고 있으며,
병사를 배치할 때는 전투력이 높은 병사가 앞쪽에 오도록 내림차순으로 배치를 하고자 한다.
다시 말해 앞쪽에 있는 병사의 전투력이 항상 뒤쪽에 있는 병사보다 높아야 한다.
또한 배치 과정에서는 특정한 위치에 있는 병사를 열외시키는 방법을 이용한다.
그러면서도 남아있는 병사의 수가 최대가 되도록 하고 싶다.
예를 들어, N=7일 때 나열된 병사들의 전투력이 다음과 같다고 가정하자.

이 때 3번 병사와 6번 병사를 열외시키면,
다음과 같이 남아있는 병사의 수가 내림차순의 형태가 되며 5명이 된다.
이는 남아있는 병사의 수가 최대가 되도록 하는 방법이다.

병사에 대한 정보가 주어졌을 때, 남아있는 병사의 수가 최대가 되도록 하기 위해서 열외해야 하는 병사의 수를 출력하는 프로그램을 작성하시오.
입력 조건
- 첫째 줄에 N이 주어진다. (1 ≤ N ≤ 2,000)
- 둘째 줄에 각 병사의 전투력이 공백을 기준으로 구분되어 차례대로 주어진다.
- 각 병사의 전투력은 10,000,000보다 작거나 같은 자연수이다.
출력 조건
- 첫째 줄에 남아있는 병사의 수가 최대가 되도록 하기 위해서 열외해야 하는 병사의 수를 출력한다.
입력 예시
7
15 11 4 8 5 2 4출력 예시
2풀이
이 문제를 해결하기 위해선, 최장 증가 부분 수열(LIS) 알고리즘에 대한 이해가 필요합니다.
‘최장 증가 부분 수열’ 문제란, 하나의 수열이 주어졌을 때, 값들이 증가하는 형태의 가장 긴 부분 수열을 찾는 문제입니다.
점화식은 아래와 같습니다.
모든 0 <= j < i 에 대하여, dp[i] = max(dp[i], dp[j] + 1) if array[j] < array[i]- dp[i] : i번째 수를 마지막 원소로 가지는 부분 수열의 최대 길이
- 0 ~ i-1번째 원소들 중에서, i번째 원소보다 작은 원소들의 dp값들 중 가장 큰 값 + 1을 dp[i]로 기록합니다.
아래 예시 배열을 통해, 최장 증가 부분 수열(LIS) 알고리즘을 이해해보겠습니다.
첫 시작은 1로 시작합니다.
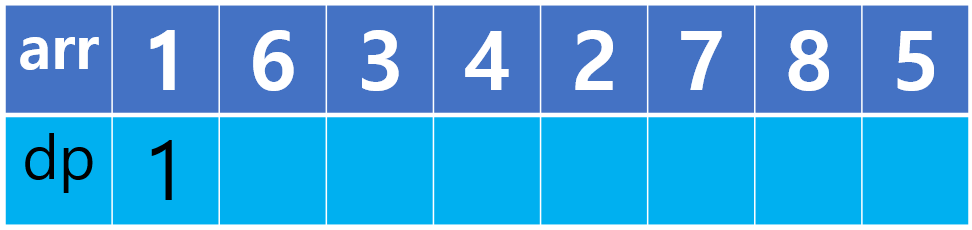
현재 값은 6이고, 6보다 작은 이전 원소들 중 가장 큰 dp값이 1이므로 1+1 = 2를 현재 dp값으로 기록합니다.

현재 값은 3이고, 3보다 작은 이전 원소들 중 가장 큰 dp값이 1이므로 1+1 = 2를 현재 dp값으로 기록합니다.

현재 값은 4고, 4보다 작은 이전 원소들 중 가장 큰 dp값이 2이므로 2+1 = 3을 현재 dp값으로 기록합니다.

현재 값은 2이고, 2보다 작은 이전 원소들 중 가장 큰 dp값이 1이므로 1+1 = 2를 현재 dp값으로 기록합니다.

현재 값은 7이고, 7보다 작은 이전 원소들 중 가장 큰 dp값이 3이므로 3+1 = 4를 현재 dp값으로 기록합니다.
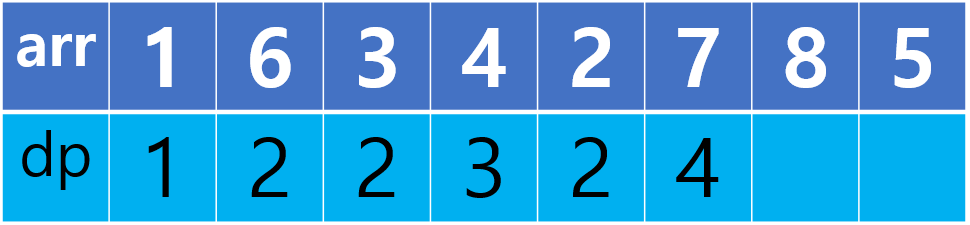
현재 값은 8이고, 8보다 작은 이전 원소들 중 가장 큰 dp값이 4이므로 4+1 = 5를 현재 dp값으로 기록합니다.
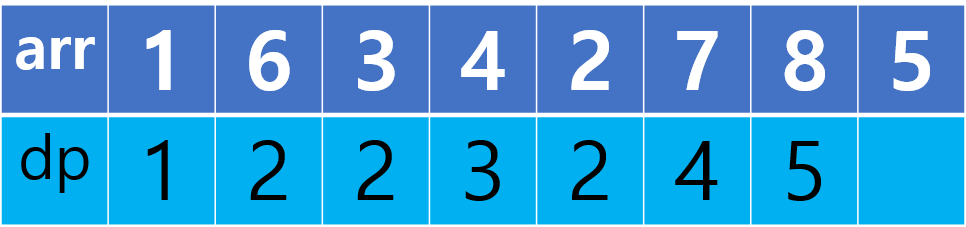
현재 값은 5이고, 5보다 작은 이전 원소들 중 가장 큰 dp값이 3이므로 3+1 = 4를 현재 dp값으로 기록합니다.

최종적으로, 테이블에 남아 있는 값 중에서 가장 큰 값이 최장 증가 부분 수열의 길이입니다.
즉, 현재 예시에서는 5가 최장 길이가 됩니다.
이제 우리가 풀어야 하는 문제를 확인해봅시다.
현재 문제는 병사를 배치할 때 전투력이 높은 병사가 앞쪽에 오도록 내림차순 배치를 하고자 합니다.
따라서 이 문제를 ‘최장 감소 부분 수열’의 길이를 계산하는 문제로 간주하고,
입력으로 주어진 원소의 순서를 뒤집은 뒤에
‘최장 증가 부분 수열’ 문제를 풀 때의 점화식을 그대로 적용하면 해결할 수 있습니다.
예제 코드
# https://www.acmicpc.net/problem/18353
import sys
n = int(sys.stdin.readline())
array = list(map(int, sys.stdin.readline().split()))
# 순서를 뒤집어 '최장 증가 부분 수열' 문제로 변환
array.reverse()
# 다이나믹 프로그래밍을 위한 1차원 DP 테이블 초기화
dp = [1] * n
# 가장 긴 증가하는 부분 수열(LIS) 알고리즘 수행
for i in range(1, n):
for j in range(0, i):
if array[j] < array[i]:
dp[i] = max(dp[i], dp[j] + 1)
# 열외해야 하는 병사의 최소 수를 출력
print(n - max(dp))참고
- 이것이 취업을 위한 코딩 테스트다. with python
- https://cocoon1787.tistory.com/713
'Algorithm > Dynamic Programming' 카테고리의 다른 글
| [DP] 이코테 “편집 거리” Python 풀이 (0) | 2022.09.21 |
|---|---|
| [DP] 이코테 “못생긴 수” Python 풀이 (0) | 2022.09.21 |
| [DP] 이코테 “퇴사” Python 풀이 (0) | 2022.09.19 |
| [DP] 이코테 “정수 삼각형” Python 풀이 (0) | 2022.09.19 |
| [DP] 이코테 “금광” Python 풀이 (0) | 2022.09.19 |

