우노
[ML] K-최근접 이웃 (K-Nearest Neighbor)이란? 본문
K-최근접 이웃 알고리즘이란?
-
K-최근접 이웃 (K-Nearest Neighbor) 알고리즘은 지도학습 알고리즘 중 하나입니다.
-
새로운 데이터를 입력 받았을 때, 해당 데이터와 가장 가까이에 있는 k개의 데이터를 확인해, 새로운 데이터의 특성을 파악하는 방법입니다.
-
아래 그림으로 자세히 살펴보겠습니다.
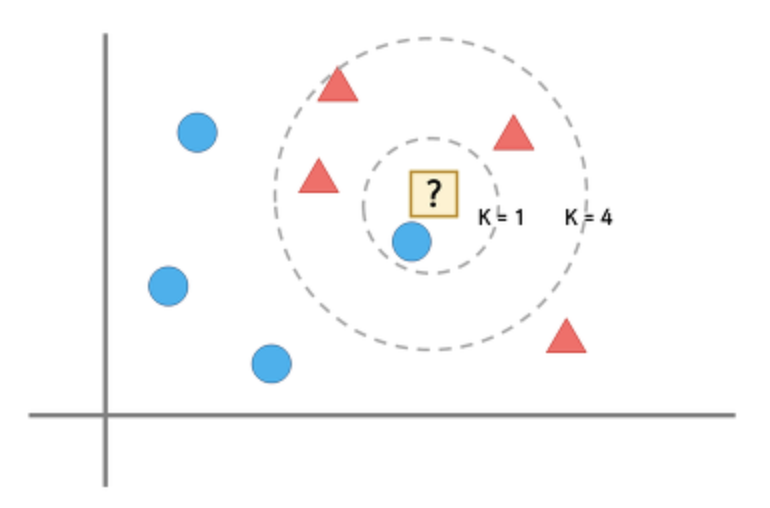
- 저 물음표에는 세모와 동그라미 중, 무엇이 들어갈까요?
- 최근접 이웃 알고리즘은 "?"의 주변에 있는 것이 동그라미이기 때문에 "?"를 동그라미라고 판단하는 알고리즘입니다.
- 매우 간단하고 직관적인 알고리즘이지만, 단순히 "?"를 가장 가까이 있는 것과 같게 선택하는 것이 옳은 분류가 될까요?
- 조금만 더 넓혀서 본다면 뭔가 부적절하다는 것이 느껴집니다.
- 따라서, 단순히 "주변에 가장 가까이 있는게 무엇인가?"가 아닌 "주변에 가장 가깝고, 많이 있는 것이 무엇인가?"라는 방식을 사용하게 됩니다.
- 이 방식을 "k-최근접 이웃 알고리즘"이라고 부르며, k는 가장 가까이에 있는 데이터의 개수를 의미합니다.
- K가 1일때는 "?" 를 파란 동그라미라고 판단하겠지만 K를 4로 변경한다면 빨간 세모라고 판단할 것입니다.
kNN의 특징
-
데이터 기반 분석 방법입니다.
- 어떤 점의 특성을 알고 싶다면 가까이 있는 점으로부터 특성 파악이 가능합니다.
-
데이터의 분포를 신경쓰지 않습니다.
-
회귀문제, 분류문제 등에 적용 가능합니다.
- 회귀 문제
- kNN의 값을 평균 내어 값 예측
- 분류 문제
- kNN 중에 가장 많은 항목 선택
- 회귀 문제
-
가까운 이웃이 여럿일 경우엔?
- 방법 1. 거리에 따라 가중치 주기
- 방법 2. 단독 1등이 나올 때까지 k를 하나씩 줄이기
-
데이터가 균일하지 않을 경우?
- cut-off를 조절
- 사전 데이터가 적은 애들한테 가중치를 준다.
- cut-off를 조절
K 선택하기
-
K는 몇으로 설정하는게 좋을까?
-
최선의 K값을 선택하는 것은 데이터마다 다르게 접근해야합니다.
- k가 낮다 → 적은 이웃 수로 판단한다 → 불안정한 결과 ~ 오버피칭
- k가 높다 → 많은 이웃 수로 판단한다 → 지나친 일반화 ~ 언더피팅
-
k를 선택하는 방법 : 가장 좋은 성능을 내는 값으로 선택
- k의 값을 1부터 증가시켜가며 각 점들에 대해 knn으로 분류해보고 오류 계산
- 가장 오류가 적은 k값을 선택
데이터간 거리 구하기
- knn은 데이터들 사이의 거리만 측정할 수 있다면 사용 가능합니다.
- 그렇다면, 데이터 간 거리를 구하는 방식은 무엇이 있을까?
- Eucledian Distance ( L2 )
- Manhattan Distance ( L1 )
- Cosine Distance
- Hamming Distance ( 곱집합)
- 자카드거리 ( 집합 )
- 그외
- Standardized Euclidean Distance
- Mahalanobis Distance
- Correlation Distance
kNN의 장단점
-
장점
- 쉽고 이해하기 직관적이다.
- 사전 학습이 필요 없다.
- 어떤 분포든 상관 없다. ( 비모수 방식)
- 데이터가 많을 경우 정확도 향상
-
단점
- 데이터가 많을 경우 연산량 증가
- 차원 축소 등으로 계산량 감소
- 인덱싱으로 탐색 속도 향상
- R-Tree, KD-Tree, KNN-Graph, LSH, etc
- 차원의 저주
- 데이터의 차원이 증가함에 따라 정확도 급하락
- 데이터가 많을 경우 연산량 증가
'AI > Machine Learning' 카테고리의 다른 글
| [ML] Epoch, Batch size, Iterations 용어 정리 (0) | 2020.07.30 |
|---|---|
| [ML] 회귀 분석 (Regression Analysis) 의 개념과 학습 흐름 (0) | 2020.07.29 |
| [ML] 생성한 데이터셋으로 다중클래스 분류 (다층퍼셉트론 모델) (0) | 2020.07.26 |
| [ML] 생성한 데이터셋으로 다중클래스 분류 (K-NN 모델) (0) | 2020.07.25 |
| [ML] Iris 데이터셋을 사용한 다중클래스 분류 (K-NN 모델) (1) | 2020.07.24 |
Comments




