우노
[ML] Metric 종류 본문
Classification Metrics (분류 메트릭)
Accuracy
- 분류기의 성능을 측정할 때 가장 간단히 사용할 수 있음
- optimize하기 어려움
Logloss
- 잘못된 답변에 대해 더 강하게 패널티 부여
Area Under Curve (AUC ROC)
- 이중 분류에만 사용된다.
- 특정 threshold를 설정
- 예측의 순서에 의존적이며 절대값엔 의존적이지 않음
Regression Metrics (회귀 메트릭)
MSE (Mean Squared Error)
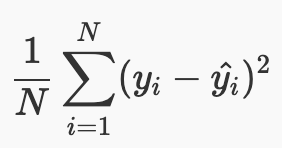
평균 오차 제곱합이라고 불리며 실제값과 오차의 차를 제곱한 뒤 평균을 한 값으로 산출한다.
예제코드
from sklearn.metrics import mean_squared_error print('MSE : ', mean_squared_error(y_test, y_pred))
RMSE (Root Mean Squared Error)

평균 오차 제곱합(MSE)에 루트를 씌운 값으로, 단순 오차 제곱합의 오차율 값이 큰 것을 보정해주며, 대표적인 회귀 척도로 많이 사용된다.
예제 코드
from sklearn.metrics import mean_squared_error def RMSE(y_test, y_pred): return np.sqrt(mean_squared_error(y_test, y_pred)) print('RMSE : ', RMSE(y_test, y_pred))
R-squared (R2)
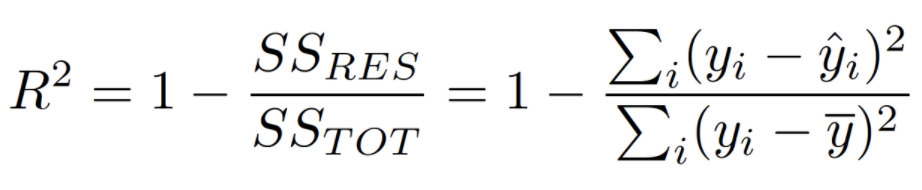
R2는 총제곱합(SST)에 대한 회귀제곱합(SSR)을 뜻하며 결정계수라고도 불린다.
결정계수는 반응변수의 변동량(분산)에서 현재 적용(만든)모델이 설명할 수 있는 부분의 비율을 뜻하며
예측의 적합도를 0과 1 사이의 값으로 계산하고, 1에 가까울 수록 설명력이 높다고 말한다.
예제 코드
from sklearn.metrics import r2_score print(' R2 : ', r2_score(y_test, y_pred))
MAE (Mean Absolute Error)

실제값과 예측값의 차이의 절대값 합의 평균이다.
MSE의 경우처럼 오류가 클수록 큰 불이익을 주지 않는다.
Outliear의 영향을 받지 않는다. (Outliear에게 robust)
예제코드
# MAE Metric def mean_absolute_error(y_test, y_pred): y_test, y_pred = np.array(y_test), np.array(y_pred) return np.mean(np.abs(y_test - y_pred)) print(' MAE : ', mean_absolute_error(y_test, y_pred))
MSE vs MAE
- MSE
- 특이값을 신경 쓰지 않아도 되는 경우
- MAE
- 특이값이 있는 경우
- 특이값에 robust를 적용해 영향을 적게 받는다.
- MSE
간단한 예를 들어보자
- 1) 예측값 : 9, 실제값 : 10 이라면 MSE = 1 이다.
- 2) 예측값 : 999, 실제값 : 1000 이라면 MSE = 1 이다.
- 1)이 더 critical 한데, MSE와 MAE는 동일한 오차로 취급한다.
위 문제점을 해결하기 위해 나온 것이 MSPE, MAPE 이다.
- MSE와 MAE의 weight 버전이라고 생각할 수도 있다.
- error를 절대적인 오차값이 아닌 오차비율로 비교한다
- relative error의 합에, 100%/N을 곱한다.
MSPE (Mean Squared Percentage Error)

MSE의 weight 버전이다.
예제코드
# MSPE def mean_squared_percentage_error(y_test, y_pred): y_test, y_pred = np.array(y_test), np.array(y_pred) return np.mean(np.square((y_test - y_pred) / y_test)) * 100 print(' MSPE : ', mean_squared_percentage_error(y_test, y_pred))
MAPE (Mean Absolute Percentage Error)
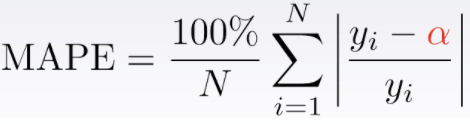
MAE의 weight 버전이다.
예제코드
# MAPE def mean_absolute_percentage_error(y_true, y_pred): y_true, y_pred = np.array(y_true), np.array(y_pred) return np.mean(np.abs((y_true - y_pred) / y_true)) * 100 print(' MAPE : ', mean_absolute_percentage_error(test_y, pred_y))
RMSLE (Root Mean Squared Logarithmic Error)
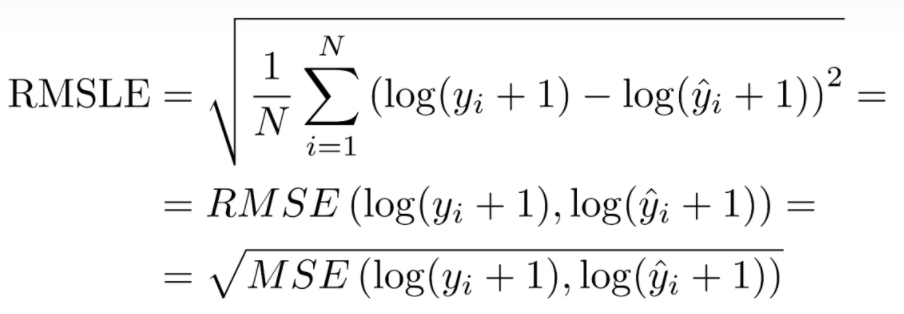
- MSPE,MAPE와 동일한 상황에 사용한다. (relative error)
- prediction value와 target value가 큰 숫자일 때, 큰 차이를 벌점으로 내고싶지 않을 때 사용한다.
- 과소평가된 항목에 패널티가 부여된다.
'AI > Machine Learning' 카테고리의 다른 글
| [ML] 이상값(outlier)과 로버스트(robust) (2) | 2020.08.06 |
|---|---|
| [ML] Model compile() - 학습과정 설정 (0) | 2020.08.06 |
| [ML] 배깅(Bagging), 부스팅(Boosting), 보팅(Voting) (0) | 2020.08.04 |
| [ML] XGBoost 개념 이해 (10) | 2020.08.04 |
| [ML] 데이터 스케일링 (Data Scaling) 이란? (8) | 2020.08.03 |


