우노
[추천시스템] Latent Factor Model 본문
- 별점 예측 부분에서 Collaborative filtering보다 동작을 잘하는게 Latent Factor Model이다.
- 하지만 단점이 존재한다.
- Collaborative filtering은 근거를 댈 수 있지만 Latent Factor Model은 근거를 댈 수 없다.
Latent Factor Model

- Latent Factor Model은 사용자와 아이템을, 잠재적인 차원(Factor)들을 사용해 나타낼 수 있다고 보는 모델이다.
- 여기서 차원은 축과 같은 의미로 사용될 수 있다.
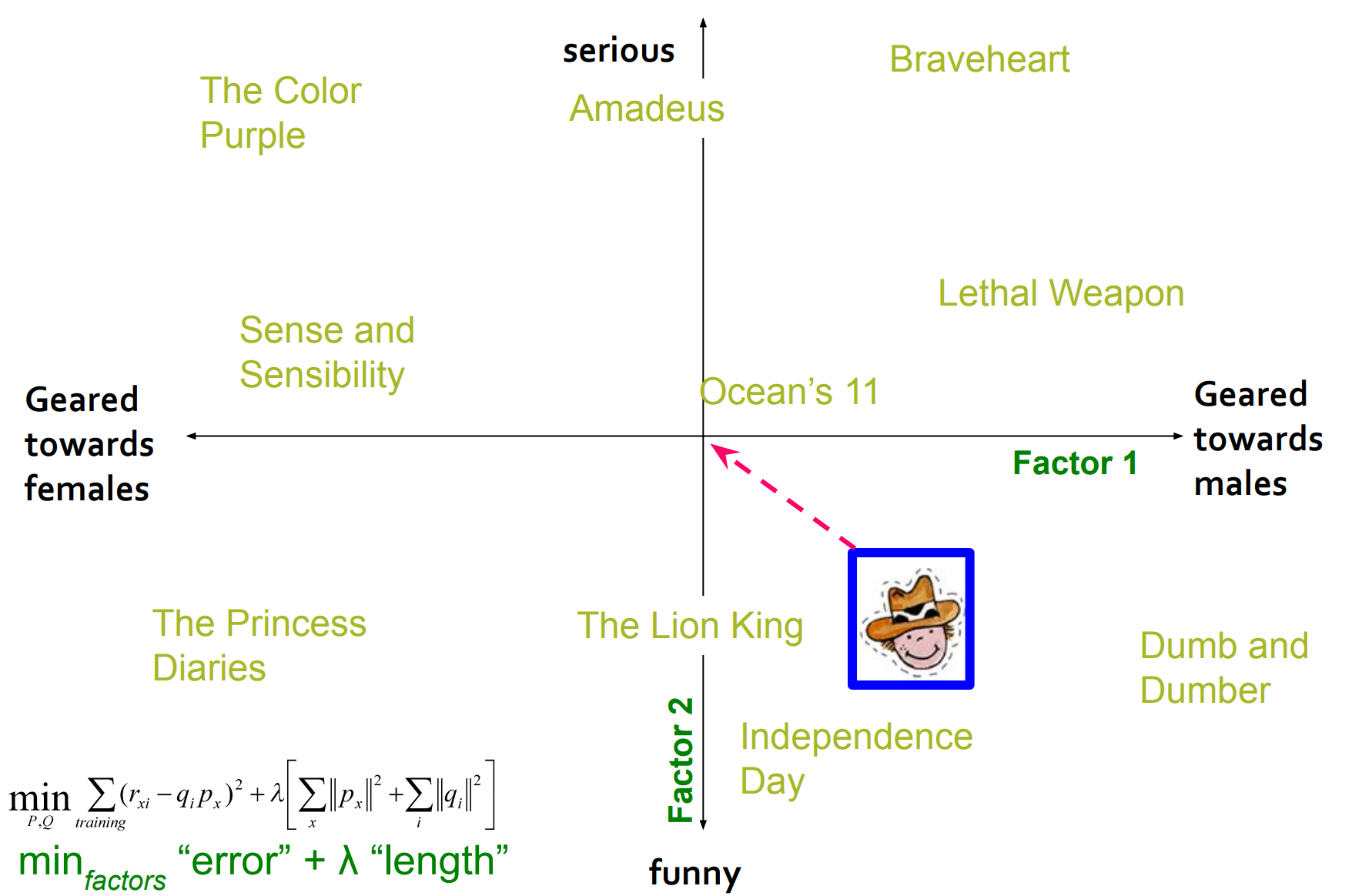
- 예를 들어, 위 그림처럼
- x 축을 남성향, 여성향의 정도로 표현하고
- y 축을 웃기고, 심각함의 정도로 표현할 수 있다면
- 사용자와 아이템은 적절한 x, y축 값에 매핑 된다는 것이다.
- 길동 = ( -3.1, -4.2 )
- 테넷 = ( 1.3, 4.5 )
- 위 예제에서는 사용자와 아이템을 두 가지 차원으로 표현했지만, 실제 Latent Factor Model에서는 사용자와 아이템을 모르는 차원에 표현한다.
- 즉, 차원이 무엇을 의미하는지 모르며
- 차원은 여러 개일 수 있다.
- 따라서, Latent Factor Model은 사용자의 매핑지점과 아이템의 매핑지점이 가까울수록 유사하다고 판단하는 모델이다.
Matrix Factorization


Matrix Factorization은 Latent Factor Model을 구현하는 방법 중 하나이다.
우선, 각 사용자와 아이템을 같은 차원의 벡터들의 집합(Matrix)으로 표현한다. ( Latent Factor Model )
- 각 차원은 무엇을 의미하는지 모르며 차원(rank)의 크기는 우리가 정할 수 있다.
- 위 그림에서는, 사용자와 아이템을 3차원 벡터들의 집합으로 표현했다.
- 처음엔 Matrix를 랜덤 값으로 아무렇게나 채워놓는다.
- 그럼, 모든 사용자와 모든 아이템에 대한 각각의 Matrix가 생기게 된다.
이제 무엇을 해야할까?
- 우리에겐 이미 존재하는 몇몇의 요소값(평점)이 있을 것이다.
- "사용자 벡터와 아이템 벡터를 내적하면 요소값(평점)이 나올것이다."라고 가정한 뒤
- (0.3, 0.4, 0.4) * (0.2, 0.3, 0.7) = 4.6
- 사용자 벡터와 아이템 벡터의 내적값(예상평점)이 실제평점값과 유사해지도록 두 개의 Matrix를 학습 시키면 된다.
- 예) 실제평점값이 5.0 이고 ( 아이템 벡터 ) * ( 사용자 벡터 ) = 4.8 라면
- 0.2 를 오차로 두고 학습한다.
가설, 비용, 업데이트


- 왼쪽 item matrix 를 p, 오른쪽 user matrix를 q라고 했을 때
- p matrix에서 i 번째 벡터는 pi
- q matrix에서 x 번째 벡터는 qx
- 1) 처음엔 각 Matrix를 랜덤 값으로 아무렇게나 채워놓는다.
- 2) 예측값을 도출하는 가설 함수는 벡터 내적을 의미하는 pi * qx로 사용한다.
- 3) 예측값과 실제값의 차이를 의미하는 비용 함수는 MSE를 사용한다.
- 4) 우리는 비용함수를 최소로 만드는 P Matrix와 Q Matrix를 찾는게 목표이다.
잘 학습 되었는지를 검증하려면?
학습 데이터(Training Set)와 검증 데이터(Test Set)를 분리해야한다.

Overfitting
실제로 학습해보면, 학습이 잘 되는가 싶다가 학습이 진행될수록
Traing error는 낮아지며
Test error는 어느정도부터 오히려 증가한다.
즉, Overfitting이 발생한다.

Regularization (정규화)
Latent vector가 너무 Training Data에 매몰되지 않도록, Latent vector가 너무 큰 값을 갖는 (범위를 벗어나는) 경우 패널티를 줘야한다.
즉, 실제값에 맞추려고 하다보면 vector 값이 너무 커질수 있다!
- 예를 들어,
- (1.0, -1.0) * (3.0, -1.0) = 4
- (10.0, -6.0) * (1.0, 1.0) = 4
- 위 벡터 내적과 아래 벡터 값은 동일한 값을 출력하지만
- 아래 벡터 값이 너무 큰 값을 갖는 것을 볼 수 있다.
- 즉, 같은 결과가 나오더라도 벡터의 절댓값들을 최소한 작게 가지고 있는게 좋다.
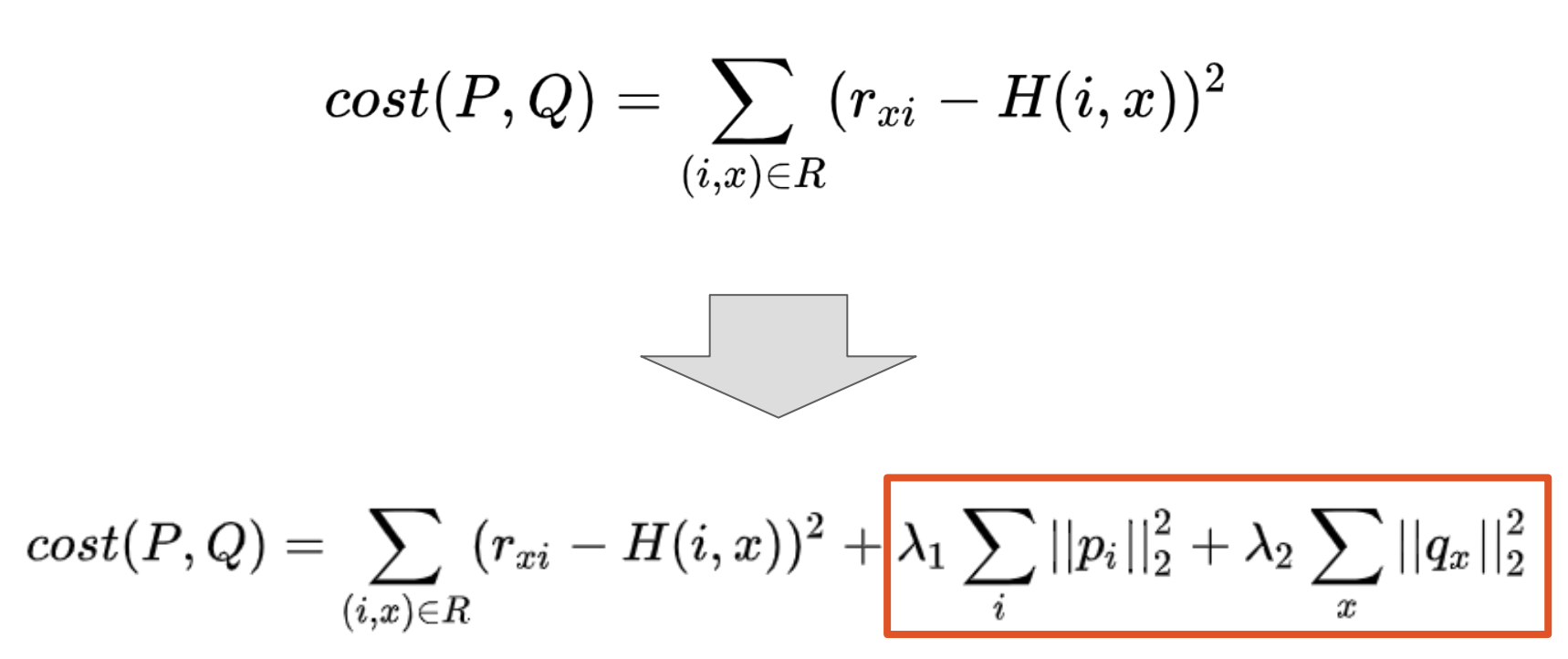
따라서, 기존의 비용함수 뒤에 추가로 L2 norm을 붙여준다.
위와 같이 cost 뒤에 Regularization을 붙이게 되면, cost가 벡터의 길이 자체를 줄이는 방향으로 움직이게 된다.
- 원점 쪽으로 벡터 값들을 땡겨온다.
- 원점으로부터 벡터 값이 너무 멀리가지 못하게 제약을 준다.
- Regularization이 없을 경우에는, 벡터가 원점에서 멀어지는 방향으로 커질 가능성이 있다.
Global Baseline Estimate
Global Baseline Estimate란 데이터가 적을 경우, 기본값을 예측하는 방식이다.
- 이미 높은 평점을 받은 드라마에는 나도 높은 평점을 주지 않을까?
- 사용자가 깐깐한 편이라면, 평균보다 조금 낮게 평점을 주지 않을까?
- 이 사용자는 기본적으로 이 정도의 평점을 줄 것이다.
Global Baseline Estimate를 사용해 문제를 해결해보자
- 문제
- 진원이는 "이태원 클라쓰"와 비슷한 드라마를 본 적이 없다.
- 진원이가 "이태원 클라쓰"를 보고 매길 평점을 예측해보자.
- 해결
- 존재하는 모든 드라마의 평점 평균 : 3.7점
- 진원이의 드라마 평점 평균 : 3.5 점 (평균보다 0.2 점 낮음)
- User Vector
- "이태원 클라쓰"의 평점 평균 : 4.2점 (평균보다 0.5점 높음)
- Item Vector
- 결과
- 기본 평점 (Global baseline) : 3.7 - 0.2 + 0.5 = 4.0
- 문제
Global Baseline Estimate는 Latent Factor model에도 적용이 가능하다.

- 기존 Latent Factor Model의 가설함수가 H(i,x) = pi * px 였다면
- Global Baseline Estimate를 적용한 Latent Factor model의 가설함수는 아래와 같다.
- H(i,x) = μ + bi + bx + pi * px
- μ : 전체 평점 평균
- bi : 아이템 i의 bias
- bx : 사용자 x의 bias
- pi * px : 아이템과 사용자의 내적값
- u는 전체 평점 평균으로 할당한 뒤
- bi, bx, pi, px 는 학습해야하는 파라미터이기에 랜덤한 값으로 초기화한다.
- 이후, cost를 구하는 과정에서 각각의 파라미터 값들이 너무 커지면 오버피팅에 일조할 수 있기 때문에, 각 파라미터에 Regularization을 같이 써줘야한다.
'Data > Recommender System' 카테고리의 다른 글
| [추천 시스템] Tensor Decomposition (0) | 2021.12.04 |
|---|---|
| [추천시스템] Latent Factor Model with Pytorch (0) | 2020.10.29 |
| [추천시스템] 유사도(Similarity) 튜토리얼 (0) | 2020.10.22 |
| [추천시스템] 추천 시스템의 개념 및 알고리즘 (0) | 2020.10.16 |
| [추천시스템] 유사도(Similarity) 구하는 방법 (0) | 2020.10.12 |
Comments


