우노
[추천 시스템] Tensor Decomposition 본문
Tensor 란?
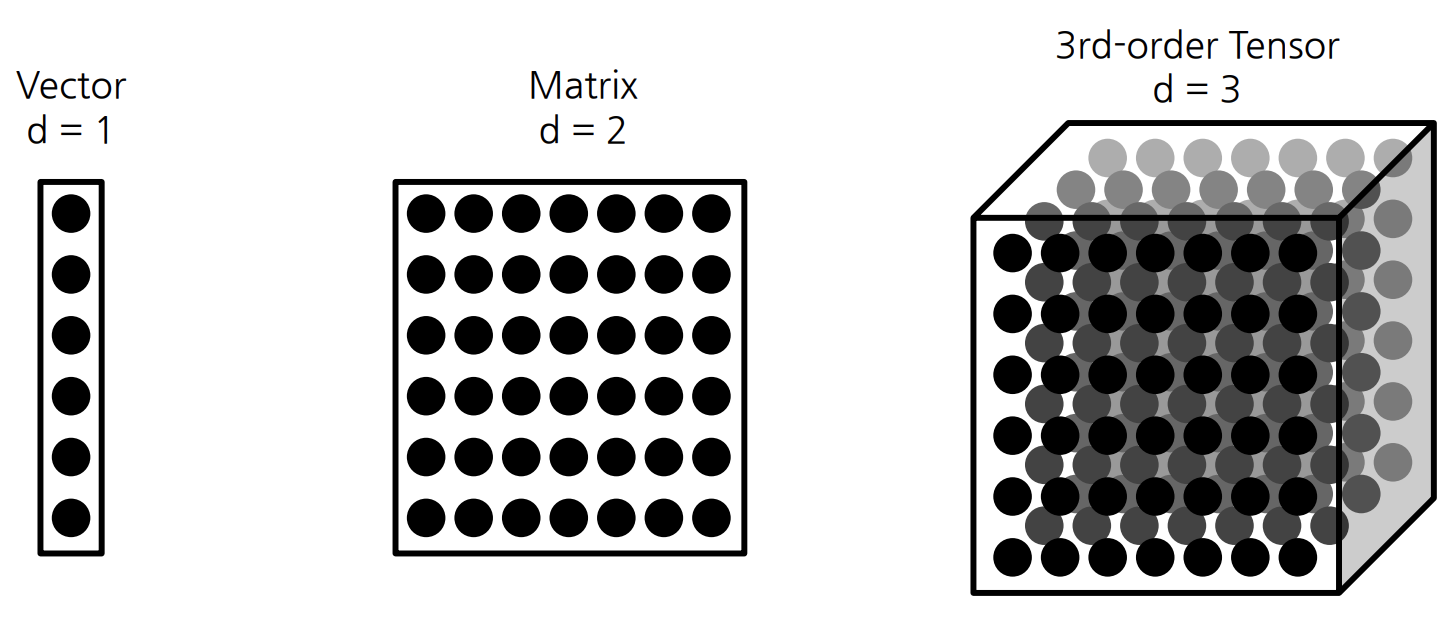
- Tensor 란, d 차원의 배열을 의미한다.
- d 가 1 이라면, First Order Tensor 이며, 이는 Vector 라고 불린다.
- d 가 2 라면, Second Order Tensor 이며, 이는 Matrix 라고 불린다.
- d 가 3 이라면, Third Order Tensor 이며, 이는 Tensor 라고 불린다.
Tensor Decomposition 이란?
우리 주위에는 아주 다양한 Tensor 데이터들이 존재한다.
- 추천 시스템
- 영화 추천, 친구 추천, 쇼핑 추천 등
- 예를 들어, x 축은 사람, y 축은 영화, z 축은 시간, value 는 평점으로 이루어진
- 어떤 사람이 어떤 영화에 어떤 시간에 어떤 평점을 주었는지에 대한 정보를 담고 있는 Tensor 가 있을 수 있다.
- 영화 추천, 친구 추천, 쇼핑 추천 등
- 데이터 압축
- 이미지 압축 등
- 데이터 분석
- 유사한 영화 찾기, 유사한 네트워크 공격 찾기 등
- 추천 시스템
이러한 Tensor 를 분해하는 작업을 Tensor Decomposition 이라고 한다.
아래 그림을 통해 Tensor Decomposition 을 이해해보자.
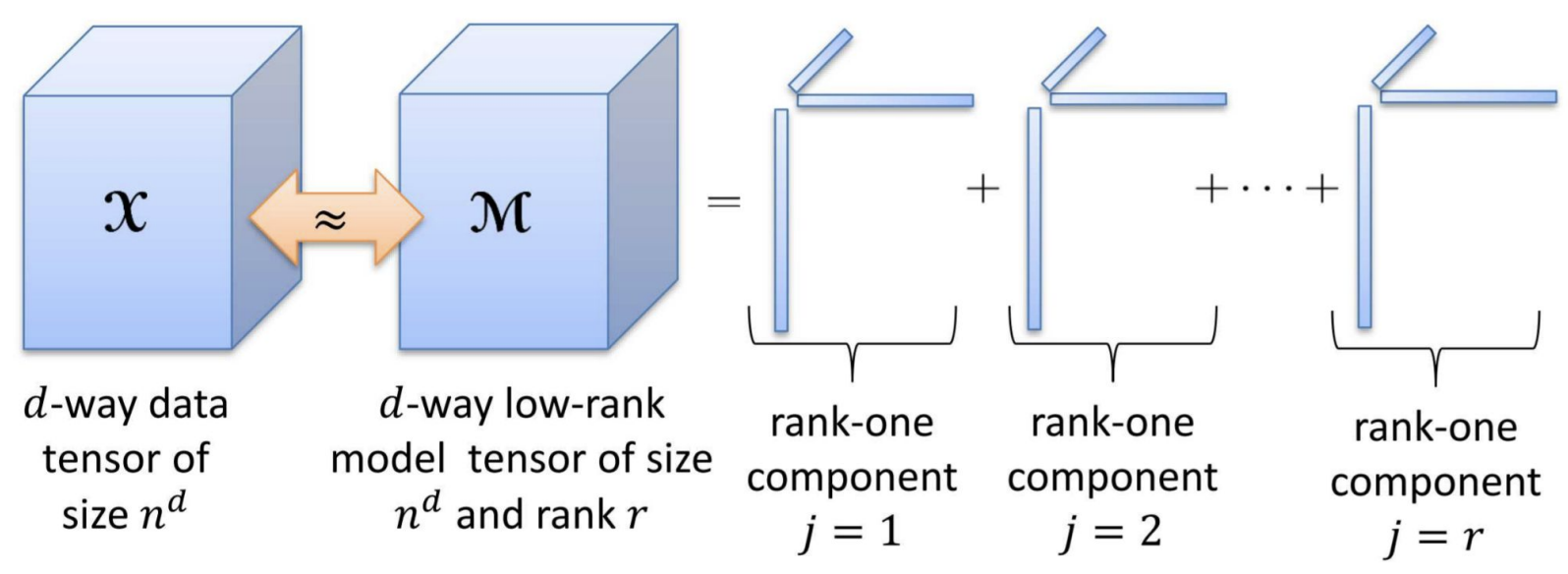
- 위 그림의 X Tensor 가 입력 데이터라면,
- 우리는 어떻게 입력 데이터 X Tensor 와 가장 유사한 M Tensor 를 구할 수 있을까?
- 우리는 여러 Vector 들의 곱의 합으로 M Tensor 를 구할 수 있을 것이다.
Tensor 보다 쉬운 Matrix 로 이해해보자.
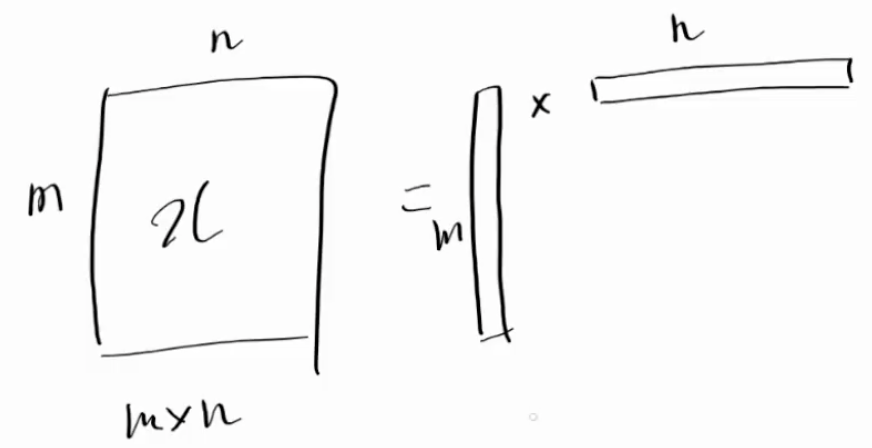
- 우리는 Vector 의 곱으로 Matrix 를 만들 수 있을까? → 당연히 만들 수 있다.
- 위의 우측 그림처럼, M Vector 와 N Vector 는 곱셈을 통해, M x N Matrix 를 만들 수 있다.
- 또한, Vector 간 곱이 좌측 M X N Matrix 와 유사해지도록, M Vector 와 N Vector 의 요소들을 학습할 수도 있다.
- 즉, 우리는 M X N Matrix 를 M Vector 와 N Vector 만으로도 표현이 가능해지며, 이를, Matrix Factorization 이라고 한다.
- 하지만, 한 번의 Vector 곱셈으로 생성된 Matrix 는, 정보량 차이로 인해, 좌측 Matrix 와 완전히 동일해질 수 없다.
- 그렇다면, 그 부족한 부분을 어떻게 해결할 수 있을까?
해당 문제는, Vector 의 곱셈을 추가적으로 더함으로써 해결할 수 있다.

- 첫 번째 Vector 곱셈만으로, 좌측 Matrix 와 최대한 유사하도록 Vector 를 학습한 뒤,
- 해결되지 않은 오차를, 나머지 Vector 곱셈을 추가함으로써 해결하는 것이다.
- 따라서, 더 많은 Vector 를 사용할 수록 Matrix 와 유사하게 만들 수 있다.
따라서, Matrix 를 표현하기 위해 사용된 Vector 곱셈 단위를 Rank 라고 하며,
Tensor 를 r 개의 Rank 로 분해한 것을, r rank Tensor Decomposition 이라고 부른다.
Tensor Decomposition 의 종류
Tensor Decomposition 의 종류는 2가지이다.

- CP-Decomposition (CANDECOMP / PARAFAC)
- 단순히, 독립적인 Factor 들의 합으로 구성함으로써, Factor 간 상관관계를 무시한다.
- Tucker Decomposition
- Core Tensor 를 통해 Factor 간 상관관계를 고려한다.
- CP-Decomposition (CANDECOMP / PARAFAC)
Outer Product 란?
아래 그림에서 a Vector 와 b Vector 를 외적하면 Matrix 가 생성되며,
해당 Matrix 에 C Vector 를 외적하면 Tensor 가 완성된다.

해당 텐서의 요소는 아래와 같이 표기된다.

Objective Functions
- CP Decomposition 과 Tucker Decomposition 의 목적 함수는 아래와 같다.
- 아래 공식에서 X 는 원래의 Tensor 를 의미하며, a, b, c 는 Vector 를 의미한다.
CP Decomposition
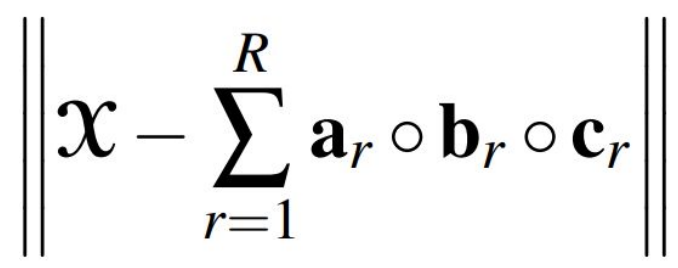
- a 와 b 와 c 의 외적은 하나의 Rank 가 되며, Rank 는 총 R 개가 존재하게 된다.
- 해당 결과를 최소로 만드는게 CP Decomposition 의 목적이며,
- Rank 의 합이 X 와 유사할수록, 목적함수의 결과는 최소가 된다.
Tucker Decomposition
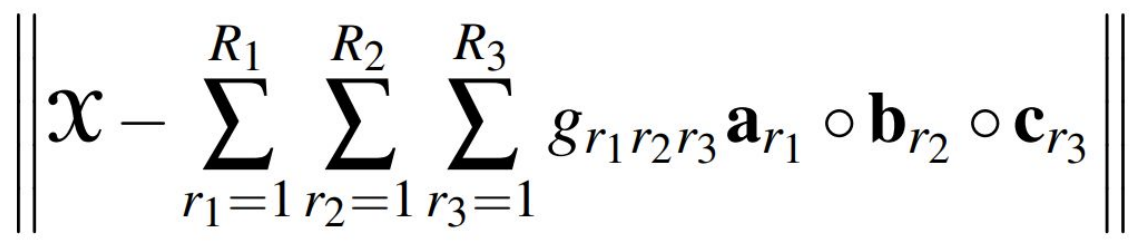

- CP Decomposition 에서는 Rank 가 r 개라면, a Vector, b Vector, c Vector 도 모두 r 개였지만,
- Tucker Decomposition 에서는 a Vector, b Vector, c Vector 의 개수가 모두 다를 수 있다.
- 위의 우측 그림처럼, a Vector 는 3 개, b Vector 는 3 개, c Vector 는 2 개 일 수 있으며, 이때의 Core Tensor 는 3 x 2 x 3 의 형태가 된다.
- Tucker Decomposition 은 각 Matrix 의 Vector 들을 조합해 외적한 뒤, 해당 결과에 Core Tensor 요소값을 곱하고, 모든 결과를 더하며 진행된다.
- 위의 우측 그림처럼, 각 Matrix 의 Vector 는 총 18개(3 x 2 x 3)의 Tensor 를 생성할 수 있으며,
- Vector 조합에 따라 Core Tensor 의 요소값을 뽑아내어, Tensor 결과에 곱하게 된다.
- 이후, 모든 결과들을 더하는 방식으로 학습하게 된다.
- (G111ㆍa1ㆍb1ㆍc1) + (G112ㆍa1ㆍb1ㆍc2) + ... + (G332ㆍa3ㆍb3ㆍc2)
CP Decomposition 과 Tucker Decomposition 의 차이점
- CP Decomposition
- 연산이 빠르다.
- 정보량이 적다.
- Tucker Decomposition
- 연산이 느리다.
- 정보량이 많다.
참고
- 국민대학교 박하명 교수님 수업 자료
- https://www.alexejgossmann.com/tensor_decomposition_tucker/
'Data > Recommender System' 카테고리의 다른 글
| [추천시스템] Latent Factor Model with Pytorch (0) | 2020.10.29 |
|---|---|
| [추천시스템] Latent Factor Model (1) | 2020.10.29 |
| [추천시스템] 유사도(Similarity) 튜토리얼 (0) | 2020.10.22 |
| [추천시스템] 추천 시스템의 개념 및 알고리즘 (0) | 2020.10.16 |
| [추천시스템] 유사도(Similarity) 구하는 방법 (0) | 2020.10.12 |
Comments


