우노
[DL] Regularization (L1, L2) 본문
-
L1 Regularization 과 L2 Regularization 을 설명하기 위한 글입니다.
-
결론부터 얘기하자면 L1 Regularization 과 L2 Regularization 모두 Overfitting(과적합) 을 막기 위해 사용됩니다.
-
위 두 개념을 이해하기 위해 필요한 개념들부터 먼저 설명하겠습니다.
-
글의 순서는 아래와 같습니다.
-
Norm
-
L1 Norm
-
L2 Norm
-
L1 Norm 과 L2 Norm 의 차이
-
L1 Loss
-
L2 Loss
-
L1 Loss, L2 Loss 의 차이
-
Regularization
-
L1 Regularization
-
L2 Regularization
-
L1 Regularization, L2 Regularization 의 차이와 선택 기준
-
Norm
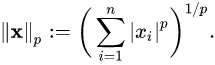
- Norm 은 벡터의 크기를 측정하는 방법입니다.
- 두 벡터 사이의 거리를 측정하는 방법이기도 합니다.
- 여기서 p 는 Norm 의 차수를 의미합니다.
- p = 1 이면 L1 Norm 이고, P = 2 이면 L2 Norm 입니다.
- n은 해당 벡터의 원소 수 입니다.
L1 Norm
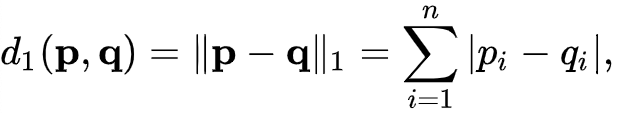
- L1 Norm 은 벡터 p, q 의 각 원소들의 차이의 절대값의 합입니다.
- 예를 들어, 두 벡터 p =(3, 1, -3), q = (5, 0, 7) 의 L1 Norm을 구한다면
- |3-5| + |1-0| + |-3 -7| = 2 + 1 + 10 = 13 이 됩니다.
L2 Norm
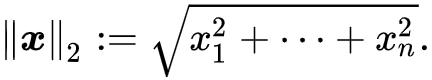
- L2 Norm 은 벡터 p, q 의 유클리디안 거리(직선 거리) 입니다.
- 여기서 q 가 원점이라면, 벡터 p, q의 L2 Norm 은 벡터 p와 원점 간의 직선거리라고 할 수 있습니다.
- 예를 들어, 두 벡터 p =(3, 1, -3), q = (0, 0, 0) 의 L2 Norm 을 구한다면
- 3^2 + 1^2 + (-3)^2 = 19 가 됩니다.
L1 Norm과 L2 Norm 의 차이

- 검정색 두 점사이의 L1 Norm 은 빨간색, 파란색, 노란색 선으로 표현 될 수 있고
- L2 Norm 은 오직 초록색 선으로만 표현될 수 있습니다.
- L1 Norm 은 여러가지 path 를 가지지만 L2 Norm 은 Unique shortest path 를 가집니다.
- 예를 들어 p = (1, 0), q = (0, 0) 일 때 L1 Norm = 1, L2 Norm = 1 로 값은 같지만 여전히 Unique shortest path 라고 할 수 있습니다.
L1 Loss
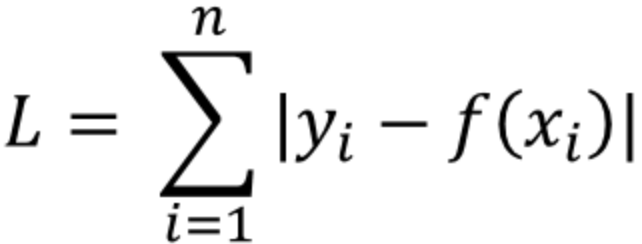
- y_i 는 실제값을, f(x_i)는 예측값을 의미합니다.
- 실제값과 예측값 사이의 오차의 절대값을 구하고, 그 오차들의 합을 L1 Loss 라고 합니다.
- 이를 Least absolute deviations(LAD), Least absolute Errors(LAE), Least absolute value(LAV), Least absolute residual(LAR), Sum of absolute deviations 라고 부릅니다.
L2 Loss

- L2 Loss 는 오차의 제곱의 합으로 정의됩니다.
- 이를 Least squares error(LSE) 라고 부릅니다.
L1 Loss, L2 Loss 의 차이
- L2 Loss 는 직관적으로 오차의 제곱을 더하기 때문에 Outlier 에 더 큰 영향을 받습니다.
- "L1 Loss 가 L2 Loss 에 비해 Outlier 에 대하여 더 Robust(덜 민감 혹은 둔감) 하다." 라고 표현 할 수 있습니다.
- Outlier 가 적당히 무시되길 원한다면 L1 Loss 를 사용하고
- Outlier 의 등장에 신경써야 하는 경우라면 L2 Loss 를 사용하는 것이 좋겠습니다.
- L1 Loss 는 0인 지점에서 미분이 불가능하다는 단점 또한 가지고 있습니다.
Regularization
- 보통 번역은 '정규화' 라고 하지만 '일반화' 라고 하는 것이 이해에는 더 도움이 될 수도 있습니다.
- 모델 복잡도에 대한 패널티로, 정규화는 Overfitting 을 예방하고 Generalization(일반화) 성능을 높이는데 도움을 줍니다.
- Regularization 방법으로는 L1 Regularization, L2 Regularization, Dropout, Early stopping 등이 있습니다.

- model 을 쉽게 만드는 방법은 단순하게 cost function 값이 작아지는 방향으로 진행하는 것입니다.
- 하지만, 이럴 경우 특정 가중치가 너무 큰 값을 가지게 될수도 있습니다.
- 가중치가 큰 값을 가진다는 것은 모델의 일반화 성능이 떨어진다는 것을 의미합니다. (과대적합)
- 위 그래프에서 actual function 이 target function 이라고 했을 때, model 이 데이터에 overfitting 된 것을 알 수 있습니다.
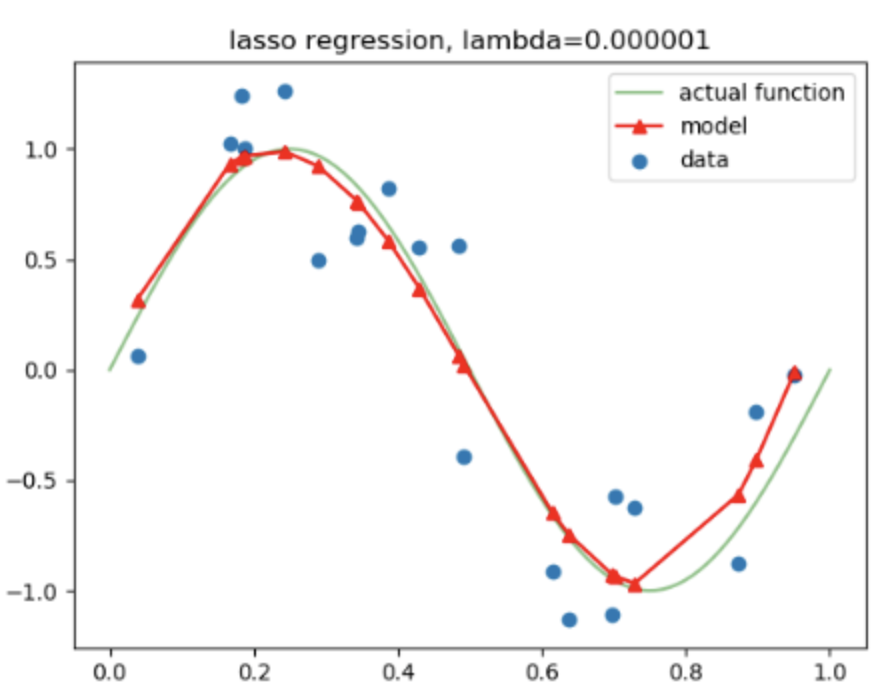
- 따라서, 위 그래프처럼 모델에 Regularization 을 적용한다면, 특정 가중치가 너무 과도하게 커지지 않게 됩니다.
L1 Regularization
-
L1 Regularization을 사용해 새롭게 정의된 cost function
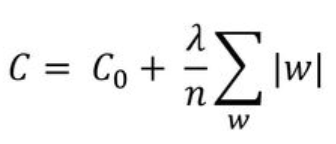
- 논문에 따라서 가중치의 절대값 앞에 분수로 붙는 1/n 이나 1/2 가 달라지는 경우가 있는데
- L1 Regularization 의 개념에서 가장 중요한 것은 cost function 에 가중치의 절대값을 더해준다는 것이기 때문에
- 1/n 이나 1/2 가 달라지는 경우는 연구의 case 에 따라 다르다고 이해하고 넘어가겠습니다. (이는 L2 Regularization 또한 같습니다).
- 기존의 cost function 에 가중치(W)의 크기가 포함되면서,
- 학습의 방향이 단순하게 cost function의 값이 작아지는 방향으로만 진행되는 것이 아니라,
- 가중치(W) 또한 작아지는 방향으로 학습이 진행됩니다.
- 이때 λ 는 상수로 0에 가까울 수록 정규화의 효과는 없어집니다.
-
새롭게 정의된 cost function을 w에 대해 편미분한 결과
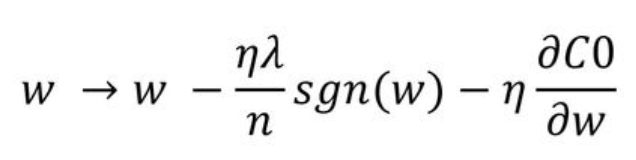
- w의 크기와 상관없이 w의 부호에 따라 상수값을 빼주는 방식
-
L1 Regularization 을 사용하는 Regression model 을 Least Absolute Shrinkage and Selection Operater(Lasso) Regression 이라고 부릅니다.
L2 Regularization
-
L2 Regularization을 사용해 새롭게 정의된 cost function

- 기존의 cost function 에 가중치의 제곱을 더함으로써
- L1 Regularization 과 마찬가지로 가중치가 너무 크지 않은 방향으로 학습되게 됩니다.
-
새롭게 정의된 cost function을 w에 대해 편미분한 결과

- w 에 ( 1-nλ/n ) 을 곱함으로써 w 값이 작아지는 방향으로 진행
- 이를 Weight decay라고 함
-
L2 Regularization 을 사용하는 Regression model 을 Ridge Regression 이라고 부릅니다.
L1 Regularization, L2 Regularization 의 차이와 선택 기준
-
L1 Regularization은 가중치 업데이트 시, 가중치의 크기에 상관 없이 상수값을 빼면서 진행됩니다.
-
때문에 작은 가중치들은 거의 0으로 수렴 되어, 몇개의 중요한 가중치들만 남게 됩니다.
-
그러므로 몇 개의 의미 있는 값을 끄집어내고 싶은 sparse model 같은 경우에는 L1 Regularization이 효과적입니다.
-
다만, L1 Regularization은 아래 그림처럼 미분 불가능한 점이 있기 때문에 Gradient-base learning 에는 주의가 필요합니다.
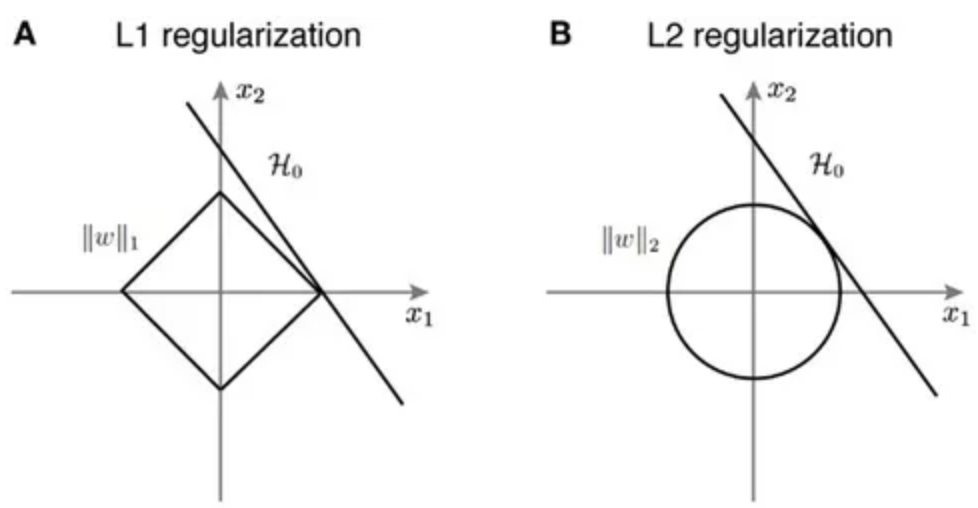
-
L2 Regularization은 가중치 업데이트 시, 가중치의 크기가 직접적인 영향을 미칩니다.
-
따라서, L2는 L1 보다 가중치 규제에 좀 더 효과적입니다.
'AI > Deep Learning' 카테고리의 다른 글
| [DL] 가중치 초기화 (1) | 2021.01.19 |
|---|---|
| [DL] Gradient Checking (1) | 2021.01.18 |
| [DL] Bias(편향) vs Variance(분산) (0) | 2021.01.17 |
| [DL] 일반적인 딥러닝 순서 (0) | 2021.01.13 |
| [DL] 간단한 순전파와 역전파 예제 (5) | 2021.01.12 |



