우노
[DL] 가중치 초기화 본문
가중치 초기화의 중요성

- Gradient Vanishing 문제란, MLP를 학습시키는 방법인 Backpropagation 중, Gradient 항이 사라지는 문제이다.
- Backpropagation 학습식을 보면 Cost Function의 Gradient 항이 존재한다.
- 이 항이 0이나 0에 가까워져 학습이 불가능해지는 현상을 말하는 것이다.
- 왜 gradient 항이 사라지는 현상이 발생할까?
- 이는 우리가 Activation Function으로 Sigmoid Function을 사용했기 때문이다.
- Sigmoid Function에 대해 자세히 살펴보자.

- Sigmoid Function의 도함수를 살펴보면 최대값이 0.25 인 것을 알 수 있다.
- 다시 말해, Sigmoid Function를 사용한다면, 망이 깊어질수록 Gradient가 1/4씩 줄어든다는 의미이다.

- 위 그림은 Backpropagation(역전파) 과정을 수식으로 나타낸것이다.
- W_1의 Gradient를 확인해보면 Backpropagation(역전파)로 인해, Sigmoid의 도함수가 중첩된 것을 볼 수 있다.
- Sigmoid의 도함수는 최대값이 0.25이기 때문에, 결국 Gradient 값이 급격히 줄어들게 되어 Gradient Vanishing 현상이 일어나게 된다.
- 하지만, 이러한 Gradient Vanishing 현상은 Activation Function의 변경을 통해 어느정도 보완할 수 있다.
- 또한, 가중치 초기화 시, 가중치의 값들을 최적의 값으로 설정한다면 gradient가 작아지더라도, 학습횟수가 적더라도 좋은 모델을 생성할 수 있다.
가중치를 0으로 초기화
- 가중치 값들을 0 으로 초기화한다면 학습이 불가능하다.
- 모든 parameter가 동일한 값으로 update 된다.
- neuron을 만드는 이유는 서로 다른 특징을 포착하기 위함인데,
- 이렇게 동일한 가중치 업데이트가 일어나면
- 여러개의 neuron을 만드는 이유, 층을 쌓는 이유가 사라진다.
- 모든 layer에 유닛이 1개인 신경망을 훈련시키는 것과 동일하다.
가중치를 random 하게 초기화
np.random.randn를 사용하면, 가중치는 평균 0, 표준편차 1인 정규분포를 따르도록 초기화된다.
이후, 작은 상수를 추가로 곱해준다.
w = np.random.randn(n_input, n_output) * 0.01곱해주는 이유는?
- 활성화함수로 sigmoid나 tanh를 사용하는 경우
- w가 크면 z가 커지고 a의 기울기 값은 작아진다.
- 따라서, gradient vanishing 문제가 발생한다.
- 활섬화함수로 ReLU를 사용하는 경우
- w가 절대값이 큰 음수 값이면 dead ReLU가 되고
- w가 절대값이 큰 양수 값이면 gradient exploding이 발생한다.
- 활성화함수로 sigmoid나 tanh를 사용하는 경우
가중치의 표준편차를 줄여서 초기화
MLP 학습시 Sigmoid 공식을 사용하며, 가중치 값들을 평균이 0이며 표준편차가 1인 정규분포를 이용해 초기화 했을 경우엔, 다음과 같이 Sigmoid 함수의 출력값이 0 과 1에 치우치게 된다.

Sigmoid 함수의 출력값이 0 과 1에 치우친다는 것은, 역전파시 기울기가 0이 된다는 뜻이다.
이를 해결하기 위한 방법 중 하나로, 가중치 값들을 표준편차가 작은 정규분포 형태로 초기화 하는 방법이 있다.
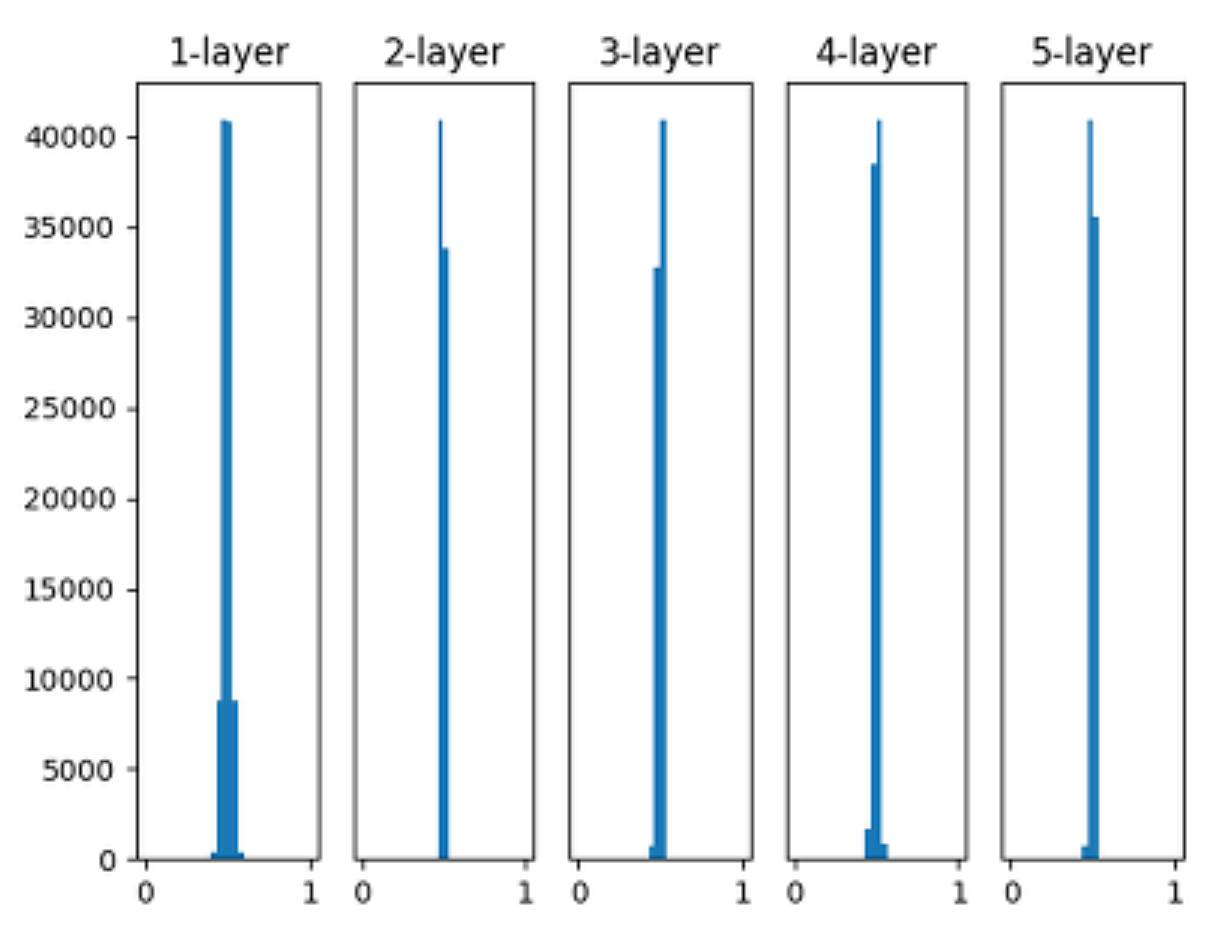
위 그림은 가중치의 표준편차를 0.01로 하는 정규분포 형태로 초기화 했을 때의 출력값들을 나타낸 그래프이다.
표준편차가 1일 때와 달리 0.5 중심으로 값이 모여 있는 것을 확인할 수 있다.
이렇게 된다면 Gradient 값이 최대 0.25 정도로 구성되어, Gradient Vanishing 현상을 완화할 수 있게 된다.
Xavier Initialization
Gradient Vanishing 현상을 완화 하기 위해서 weight 를 초기화 할 때,
Sigmoid와 같은 S자 함수의 경우, 가장 중요한 것은 출력값들이 표준 정규 분포 형태를 갖게 하는 것이다.
출력값들이 표준 정규분포 형태를 갖게 되어야 안정적으로 학습이 가능하기 때문이다.
Xavier(사비에르) Initialization 방법은, 단순히 가중치를 작은 값의 표준편차를 갖는 형태로 초기화 하는 것이 아닌, 보다 발전된 방법이다.
Xavier Initialization 방법은 표준 정규분포로 초기화 된 가중치를 1/입력개수 제곱근으로 나누어주면 된다.
w = np.random.randn(n_input, n_output) / sqrt(1/n_input)아래 그래프는 활성화함수로 Sigmoid, 가중치 초기화로 Xavier Initialization 방법을 사용했을 경우의 그래프이다.

- 10층 레이어에서도 출력값들이 표준 정규분포 형태로 잘 출력되고 있는 것을 알 수 있다.
아래 그래프는 활성화함수로 ReLU, 가중치 초기화로 Xavier Initialization 방법을 사용했을 경우의 그래프이다.

- 출력값이 0으로 수렴하고 평균과 표준편차 모두 0으로 수렴하는 모습을 확인할 수 있다.
- 즉, ReLU 함수를 사용할 경우에는 가중치 초기화로 Xavier Initialization 방법을 사용할 수 없다는 의미이다.
He Initialization
ReLU에 맞는 가중치 초기화 방법이다.
He Initialization은 Xavier Initialization와 크게 다르지 않다.
표준 정규분포로 초기화 된 가중치를, 2/입력개수 제곱근으로 나누어주면 된다.
He가 Xavier의 2배가 되는 제곱근을 사용하는 이유는
ReLU는 입력이 음수일 때, 출력이 전부 0이기 때문에 더 넓게 분포시키기 위해서이다.
w = np.random.randn(n_input, n_output) / sqrt(2/n_input)
아래 그래프는 활성화함수로 ReLU, 가중치 초기화로 He Initialization 방법을 사용했을 경우의 그래프이다.

10층 레이어에서도 평균과 표준편차가 0으로 수렴하지 않는 것을 알 수 있다.
결론
- 가중치를 0으로 초기화하는 것은 금지
- 활성화함수로 Sigmoid나 Tanh를 사용할 경우에는 Xavier 초기화 사용
- 활성화함수로 ReLU를 사용할 경우에는 He 초기화를 사용
'AI > Deep Learning' 카테고리의 다른 글
| [DL] 지수 가중 평균 (Exponentially Weighted Averages) (1) | 2021.01.20 |
|---|---|
| [DL] Regularization (Dropout) (0) | 2021.01.19 |
| [DL] Gradient Checking (1) | 2021.01.18 |
| [DL] Regularization (L1, L2) (0) | 2021.01.18 |
| [DL] Bias(편향) vs Variance(분산) (0) | 2021.01.17 |




